2

A year ago I asked [this] (Proving a few properties of Bertrand curves) same question (without the "why can't a curve be a Bertrand mate of itself" part) - see that post if you want to know the essential definitions - and gave a partial answer to the first question (I showed it was constant, but hand-waved away a sign in the last step). At the time I was a lot less mature so I made a few steps that currently seem unjustified, and unfortunately even now I seem to be unable to correct them, which is why I'm asking this question. Before I did that, however, I tried to find other solutions besides my own partial one and found this on Kreyszig's differential geometry book, which is essentially what I wrote on the other post, but more direct:

enter image description hereenter image description here

where the following notation is used: $t^{*}$ is the tangent vector to $x^{*}$, which is a Bertrand mate to $x$, $p$ is the normal vector to $x$. The * just mean we're talking about vectors tangent/normal/binormal to $x^{*}$ instead of $x$. That being said, my questions are:

  • Isn't the correct expression given by $t^{*} = t \cos(\alpha) \pm b \sin(\alpha) $? After all, $t^{*} = \langle t^{*}, t \rangle t + \langle t^{*}, b \rangle b $, and $\langle t^{*}, b \rangle ^2 = \sin^2(\alpha)$, since $\langle t^{*}, t^{*} \rangle = 1$, where $\langle t, t^{*} \rangle = \cos(\alpha)$ by definition. Also, in that case what determines the $\pm$ sign, and how?

    • What, if any, are the problems in assuming $\alpha$ is a Bertrand mate of itself, that is, $a = 0$? Is it just uninteresting or is there some other unwanted complication?
Matheus Andrade
  • 6,998

1 Answers1

1

If you allow the curve itself to be a Bertrand mate, results like this will be blatantly false. What's more, the thing that characterizes curves that have a Bertrand mate is the equation $$a\kappa+b\tau = 1$$ for some nonzero constant $a$ and constant $b$.

I agree that the equation should not have the $\pm$ in front, since, as you point out $\cos\alpha = \mathbf t\cdot\mathbf t^*$.

Ted Shifrin
  • 125,228
  • That's obvious (even though there may be some cases where they're still true, like circular helices), I guess there's nothing more io it than that. Do you have anything to comment on the other part of the question (determining the coefficients of $t^{*}$?) I'd appreciate that, it's something really small but it still bothers me. – Matheus Andrade May 04 '19 at 01:49
  • 1
    I'm always wary of responses as Answers that are significantly shorter than the corresponding Questions. Perhaps you could state your point in a fuller fashion? – hardmath May 04 '19 at 02:13
  • 1
    I have expanded on the answer. It was in fact a valid answer to the main question. As an experienced MSE user (and one who has answered many of the OP's questions), I resent all this sniping. – Ted Shifrin May 04 '19 at 06:06
  • @TedShifrin Your resentment is completely justified, the sniping is really annoying and I was gonna accept your answer anyway (it was indeed a valid one). Thanks a lot! Really appreciate it.

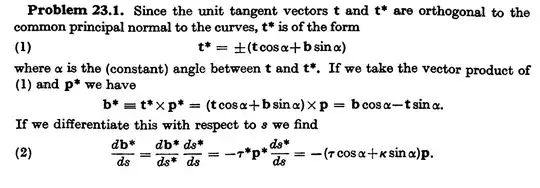
    Also, my proof was right but I forgot to take care of a lot of signs. A friend showed me his resolution and I know where I went wrong there.

    (also, I have moved on to a lot more stuff since that question, I'm not still solely studying curves hahaha, this question was really just for peace of mind)

     – Matheus Andrade May 04 '19 at 21:04
  • Thanks, Matheus. I'll look for questions on higher dimensions now :) – Ted Shifrin May 04 '19 at 21:27