1

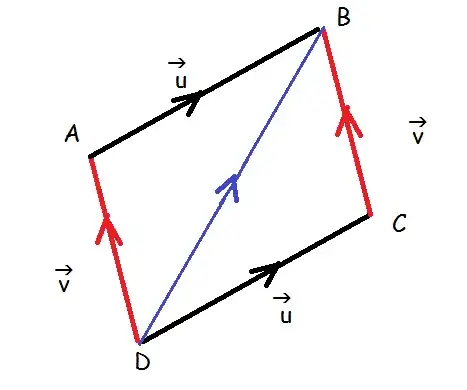
I would like to show the commutativity property of vector addition:

$$\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u},$$ without using coordinates.

I know that the idea is to properly represent $\overrightarrow{u}$ and $\overrightarrow{v}$. Writing $$\overrightarrow{u}=\overrightarrow{AB}\quad \textrm{and}\quad \overrightarrow{v}=\overrightarrow{BC}$$ it follows $$\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{AC}.$$

Now, given $\overrightarrow{v}$ and the point $A$ there exists a unique point $D$ such that $$\overrightarrow{v}=\overrightarrow{AD}.$$ Also, given $\overrightarrow{u}$ and the point $D$ there exists a unique point $C^\prime$ such that $$\overrightarrow{u}=\overrightarrow{DC^\prime}.$$ It suffices to show that $C=C^\prime$, for in this case:

$$\overrightarrow{v}+\overrightarrow{u}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}.$$ Geometrically, it is clear that $C=C^\prime$ but how to prove it?

Thanks.

PtF
  • 9,895

2 Answers2

1

I am lazy and will not put arrows above everything...

You can prove it geometrically:

The vectors $u,v$ span a plane, so we can reduce everything to a 2D problem (or use geometrical results for arbitrary dimensions, whichever you prefer).

In this plane, we have the points $A,B,C,D,C'$. Now $AD$ and $BC$ are represented by the same vector $v$, meaning that these are parallel lines of same length. Same goes for $AB$ and $DC'$. Thus, $A,B,C,D$ and $A,B,C',D$ both form parallelograms with matching edge lengths and three of the fours points coinciding. Then, of course, also the last point $C = C'$ has to be the same.

Dirk
  • 6,509
0

Consider a parallelogram ABCD.

Let $\overrightarrow{DC} = \overrightarrow{u}$ and $\overrightarrow{CB} = \overrightarrow{v}$. Thus, $\overrightarrow{DB} = \overrightarrow u + \overrightarrow v ...(i)$. enter image description here

Now as $\overrightarrow {AB} || \overrightarrow{DC}$. So, $\overrightarrow{AB} = \overrightarrow u$.

Similarly, $ \overrightarrow{DA} = \overrightarrow v$.

So, $\overrightarrow{DA} + \overrightarrow{AB} = \overrightarrow{v} + \overrightarrow{u} = \overrightarrow{DB} ...(ii)$.

As, $\overrightarrow{DB}$ is unique, from (i) and (ii),

$$\overrightarrow{u}+\overrightarrow{v} = \overrightarrow{v}+ \overrightarrow{u}$$

19aksh
  • 12,835