Burgers' equation - Integrate discontinuity over rectangle

Question

I am studying conservation laws and hyperbolic systems, particularly, Burgers' equation and shocks, and have a doubt at page 40 of the book Numerical Methods for Conservation Laws by R.J. LeVeque (Birkäuser, 1992).

I could not understand the following calculation:

If a discontinuity is present, then integrating $(u^2)_t + (\frac{2}{3}u^3)_x$ over an infinitesimal rectangle as in Figure 3.12 gives $$\int_{x_1}^{x_2}u^2(x,t)\, dx \bigg|^{t_2}_{t_1} + \int_{t_1}^{t_2}\dfrac{2}{3}u^3(x,t)\, dt \bigg|^{x_2}_{x_1} = s_1\Delta t(u_l^2-u_r^2)+\dfrac{2}{3}\Delta t (u_r^3-u_l^3)+O(\Delta t^2)$$

where

We took an infinitesimal rectangle over a shock and have $s_1=\tfrac{1}{2}(u_l+u_r)$. Here, $u_l$ is the solution of $u(x,0)$ at left of $x=0$ and $u_r$ is the value at right (Riemann problem).

$O(\Delta t^2)$ means some quantity depending of $\Delta t^2$ ($<C\Delta t^2$ for some $C>0$, is it right?), but I could not understand the calculation very well. Can somebody explain this?

Answer 1

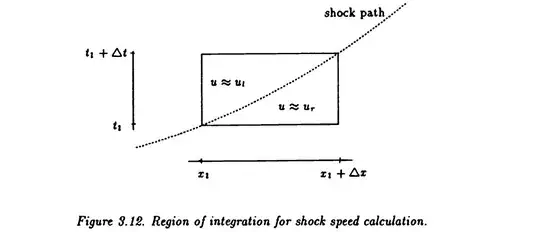
Note that the shock speed is not constant here, which explains the $\approx$ symbols and the nonlinear shock path in Fig. 3.12. In the book, it is written that

Assuming that $u$ is smoothly varying on each side of the shock, and that the shock speed $s(t)$ is consequently also smoothly varying, we have the following relation between $\Delta x$ and $\Delta t$: $$ \Delta x = s(t_1) \Delta t + O(\Delta t^2) . \tag{3.37} $$

which is nothing else but a Taylor series of the shock path $x_s(t)$ at $t=t_1$: $$ x_s(t_1 + \Delta t) = x_s(t_1) + s(t_1) \Delta t + O(\Delta t^2) , $$ where $s(t_1) = x'_s(t_1)$ is the speed of shock and $\Delta x = x_s(t_1 + \Delta t) - x_s(t_1)$. If $u$ is smoothly varying on each side of the shock, we deduce from Taylor series that $$ u(x,t)^n = \left\lbrace \begin{aligned} &{u_l}^n + O(\Delta t) & &\text{if}\quad x<x_s(t)\\ &{u_r}^n + O(\Delta t) & &\text{if}\quad x>x_s(t) \end{aligned} \right. $$ for all $n$ (see also textbook after Eq. $(3.38)$). Note that one can replace $O(\Delta t)$ by $O(\Delta x)$ in the previous equation, according to $(3.37)$. Integrating $(u^2)_t + (\frac23 u^3)_x$ over the region of integration $\mathcal{D} = [x_1, x_2]\times [t_1, t_2]$ with $x_2 = x_1+\Delta x$ and $t_2 = t_1+\Delta t$, we have on the one hand \begin{aligned} \iint_{\mathcal D} (u^2)_t \,\text dt\text dx &= \int_{x_1}^{x_2} u^2\,\text dx \bigg|_{t_1}^{t_2} \\ &= \Delta x \left({u_l}^2 - {u_r}^2\right) + O(\Delta t \Delta x) \\ &= s_1 \Delta t \left({u_l}^2 - {u_r}^2\right) + O(\Delta t^2) . \end{aligned} On the other hand, \begin{aligned} \iint_{\mathcal D} (\tfrac23 u^3)_x \,\text dx\text dt &= \int_{t_1}^{t_2} \tfrac23 u^3\,\text dt \bigg|_{x_1}^{x_2} \\ &= \tfrac{2}{3} \Delta t \left({u_r}^3 - {u_l}^3\right) + O(\Delta t^2) , \end{aligned} which yields the result.

---

Here, we have used the fact that if $f(t) = O(\Delta t)$ is a continuous function of $t$ over $[t_1, t_1+\Delta t]$, then according to the definition of $O(\Delta t)$, there exists $M > 0$ and $C\geq 0$ such that $|f(t)| \leq C \Delta t$ for all $\Delta t < M$ and all $t$ in $[t_1, t_1+\Delta t]$. The integral $I = \int_{t_1}^{t_1+\Delta t} f(t)\, \text d t$ satisfies $$ \left|I\right| \leq \int_{t_1}^{t_1+\Delta t} \left| f(t)\right| \text d t \leq C \Delta t \int_{t_1}^{t_1+\Delta t} \text d t , $$ and thus, $I = O(\Delta t^{2})$ (see also this post).