5

Let $X,Y$ be two path-connected topological spaces and $\langle A\mid R\rangle,\langle B\mid S\rangle$ respectively presentations for their fundamental groups. I think that a presentation for the fundamental group of the wedge sum $X\vee_{x_{0}} Y$ is $\langle A\sqcup B\mid R,S\rangle$.

All one should prove is that if $f$ is a loop in $X$ and $g$ a loop in $Y$ (both with base-point $x_{0}$) such that $f\cdot g\simeq g\cdot f$ in $X\sqcup Y$, then at least one of the two loops is homotopic to $x_{0}$ in his own space. How can I prove this?

I'd tried taking a homotopy $H$ between $f\cdot g$ and $g\cdot f$, and analize the possible preimages by $H$ of $x_{0}$. I saw that these preimages must contain curves of this form or similar:

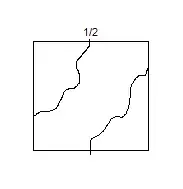
enter image description here

and this could give the needed homotopy.

I'm not sure that this reasoning is right and how to complete. Can anyone help me please? Thank you very much.

Her
  • 105
  • 1
    I doubt this is true as stated: I think you'll need some sort of local regularity condition at the basepoints. – Chris Eagle Mar 04 '13 at 22:04
  • You need some mild hypotheses on what a neighborhood of $x_0$ looks like, but you can prove a version of this using Seifert-van Kampen (http://en.wikipedia.org/wiki/Seifert%E2%80%93van_Kampen_theorem). – Qiaochu Yuan Mar 04 '13 at 22:07

1 Answers1

8

The question is whether $\pi_1 : \mathsf{Top}_* \to \mathsf{Grp}$ preserves coproducts. When $x_0$ has a connected weakly contractible open neighborhood in both spaces which are connected, then it is true by the Seifert van Kampen theorem. In general it is wrong, take $X=Y=$ Hawaiian earring.

Martin Brandenburg
  • 181,922
  • In this example clearly the hypothesis mentioned don't hold, but why this contradicts my affirmation? The $\pi_{1}$ of the Hawaiian earring, is the free group generated by an infinite countable set or am I wrong? – Her Mar 05 '13 at 01:20
  • 2
    @Her: no, $\pi_1$ of the Hawaiian earring is much more complicated. The Hawaiian earring is not a wedge sum of countably many circles; it inherits the subspace topology from $\mathbb{R}^2$ and in particular you can write down some "infinite products" of the obvious loops. – Qiaochu Yuan Mar 05 '13 at 05:30
  • I personally wanted a proof to go with this statement, so here is a paper with some useful information. http://www.math.byu.edu/~conner/research/he_main.pdf Page 14-15 has clear example of $\pi_1$ not preserving coproducts – Jack Davies Nov 05 '14 at 07:27