Using a Lyapunov function to classify stability and sketching a phase portrait

Question

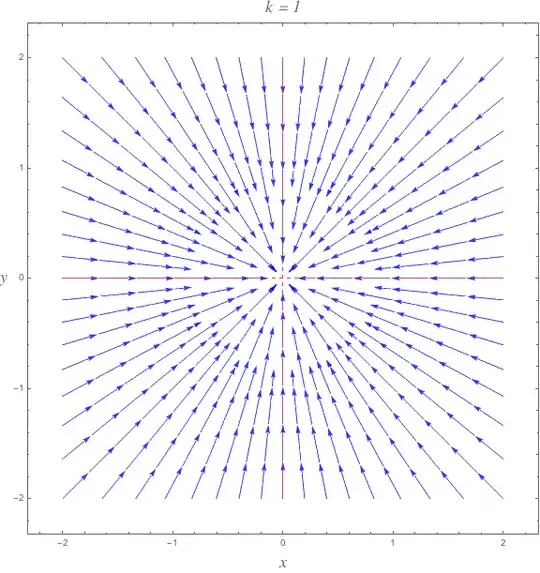
Consider the system $$x' = -x^3-xy^{2k}$$ $$y' = -y^3-x^{2k}y$$ Where $k$ is a given positive integer.

a.) Find and classify according to stability the equilibrium solutions.

$\it{Hint:}$ Let $V(x,y) = x^2 + y^2$

b.) Sketch a phase portrait when $k = 1$

$\it{Hint:}$ What are $x'$ and $y'$ when $y=ax$ for some real number $a$?

a.) Using $V$, we get $\frac{d}{dt}V=2xx'+2yy'$

Plugging in our system , we get:

$$\frac{d}{dt}V=2x(-x^3-xy^{2k})+2y(-y^3-x^{2k}y)$$ $$=-(x^4+y^4)-x^2y^{2k}-x^{2k}y^2<0$$ I dropped the $2$ since it doesn't matter to determine stability. We see that our own equilibrium is $(0,0)$ since setting $x'=0$ we get $$y^{2k}=-x^2$$ Which only works for $x=y=0$

Therefore our system is asymptotically stable at the origin.

I am having trouble with b.), mostly because the hint is confusing me.

Let $y=ax$, then our system becomes $$x'=-x^3-a^2x^3=-x^3(1+a^2)$$ $$y'=-a^3x^3-ax^3=-ax^3(1+a^2)$$ I am not sure what to do with this. Using linearization doesn't work since the Jacobian will be the zero vector at the point of interest. I have never had a problem that asks to draw a phase portrait when linearization doesn't work, so I am hoping someone more clever than me can offer some advice.

Answer 1

Although there are many ways to do this, I suspect what the problem is guiding you towards doing is to obtain the flow directly by evaluating over every line that intersects the origin in phase space.

So for a sketch, you would draw the line $y = 0.1 x$, and use the expression you found above for $a = 0.1$ to determine the magnitude and direction of the flow on that line. Then try it for a couple of other different lines, and use common sense to fill in the rest.

Answer 2

Phase portraits - a partial offering

Below are phase portraits for $k=1,2,5$. The red lines indicate the null clines where $\dot{y}=0$ and $\dot{y}=0$.

$k = 1$

The linear system is

$$\begin{align} \begin{split} \dot{x} &= -x^{3} - xy^{2} = -x \left( x^{2} + y^{2} \right) \\ \dot{y} &= -y^{3} - x^{2}y = -y \left( x^{2} + y^{2} \right) \end{split} \end{align}$$

$$ \dot{r} = \frac{x \dot{x} + y \dot{y}}{r} = -r^{3} $$

The lone critical point is the origin.

When $y = a x$, $a\in\mathbb{R}$, we have $$\begin{align} \begin{split} \dot{x} &= -x^{3}\left( 1 + a^{2} \right) \\ \dot{y} &= -a y^{3}\left( 1 + a^{2} \right) \end{split} \end{align}$$

$k = 2$

$$\begin{align} \begin{split} \dot{x} &= -x^{3} - xy^{4} = -x \left( x^{2} + y^{4} \right) \\ \dot{y} &= -y^{3} - x^{4}y = -y \left( x^{2} + y^{2} \right) \end{split} \end{align}$$

$$ \dot{r} = \tfrac{1}{8} r^3 \left(\left(r^2-2\right) \cos (4 \theta )-r^2-6\right) $$

The bounding curves for $\dot{r}$ are when $\cos 4\theta = 1$

$$\dot{r} = -r^{3}$$

and when $\cos 4\theta = -1$

$$\dot{r} = -\tfrac{1}{4} r^3 \left(r^2+2\right)$$

The bounding curves cross at $r=\sqrt{2}$. At no point is $\dot{r}$ ever positive.