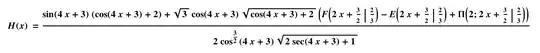CAS integrals of discontinuous functions

Question

Background

This post is motivated by my interest in the performance of symbolic integrators in computer algebra systems (CAS's), such as Mathematica (MMA).

I've found that, when an integrand has discontinuities, the indefinite integral returned by MMA often has discontinuities that don't match locations with those in the integrand itself (i.e., they occur at different points in the domain). Here is an example taken from a WRI (Wolfram Research Institute, the maker of MMA) blog (https://blog.wolfram.com/2008/01/19/mathematica-and-the-fundamental-theorem-of-calculus/):

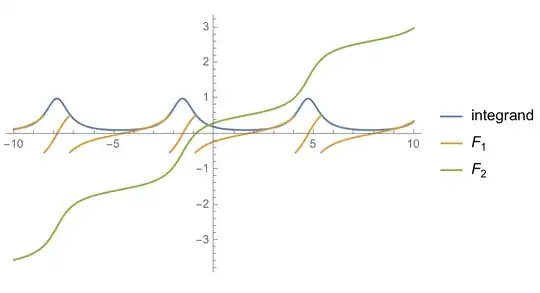
Consider the integrand: $$f(x) = \frac{1}{4 \sin (x)+5}$$

$f$ is continuous over the reals, but has poles in the complex plane at $x = \pi (2 n-\frac{1}{2}) \pm i \ln(2)$, where $n \in Z$.

MMA returns the following indefinite integral:

$$F_1(x)=\frac{1}{3} \left(\tan ^{-1}\left(2-\frac{3}{\tan \left(\frac{x}{2}\right)+2}\right)-\tan^{-1}\left(2-\frac{3}{\cot \left(\frac{x}{2}\right)+2}\right)\right)$$

While $f$ is continuous on the reals, $F_1$ is not. By comparison, the following indefinite integral is continuous on the reals (see picture below):

$$F_2(x) = \frac{x}{3}+\frac{2}{3} \tan^{-1}\left(\frac{\cos (x)}{\sin (x)+2}\right)$$

As the blog author explains, $F_1$ and $F_2$ differ by a piecewise constant.

[Interestingly, Rubi (https://rulebasedintegration.org), developed by Albert Rich, and available as add-on integration package for MMA, does return $F_2$.]

An implicit message of the blog seems to be that $F_1$'s discontinuities on the reals do not make it an inferior result to $F_2$, since if the integrand has discontinuities, discontinuities somewhere in the antiderivative are unavoidable: "Moreover, if a meromorphic integrand $h(z)$ has simple poles in the complex plane, it is impossible to choose an antiderivative $\mathcal{H}(z)$ continuous along every imaginable path in the complex plane–because of branch cuts in $\mathcal{H}(z)$."

Specifically, the author explains that while $F_1$ may have discontinuities in the reals that aren't present in $F_2$, $F_2$ has discontinuities elsewhere in the complex plane that aren't present in $F_1$. For instance, he shows that $F_2$ has a discontinuity at $x = \frac{3}{2} + i \ln(2)$, while $F_1$ does not. I.e., you have to pay somewhere.

However (and this is what motivates my questions), I disagree with that message (that $F_1$ and $F_2$ are equivalent because they both have discontinuities). Instead, I think it is functionally superior to have an antiderivative whose discontinuities occur only where there are also discontinuities in the integrand. For instance, if the integrand is continuous on the reals, it is convenient to have an antiderivative that is likewise continuous along the reals, so that one does not have to do a piecewise integration there. [Note also that $F_2$'s discontinuity at $x = \frac{3}{2} + i \ln(2)$ matches that of $f$.]

Questions

[Note: Based on Robert Israel's answer, I've edited my question to improve it.]

As I understand it, if an integrand has certain types of discontinuities, one cannot avoid discontinuities in its antiderivatives.

Further, not every function has an antiderivative. But: Suppose we have a discontinuous integrand for which a continuous-everywhere antiderivative can't exist (because of the nature of the discontinuities in the integrand) (such as $f$, above). Further suppose a non-piecewise antiderivative (i.e., one with a single functional form) for this integrand does exist, but that it has discontinuities that don't match up to those of the integrand (e.g., $F_1$). In such cases, must there also exist a non-piecewise antiderivative whose discontinuities do match the locations of those of the integrand (e.g., $F_2$)?

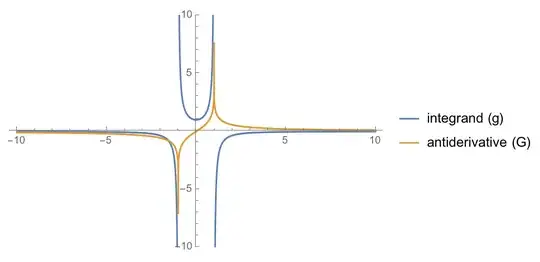
For example, consider the integrand:$$g(x) = \frac{x^2+1}{\left(1-x^2\right) \sqrt{x^4+x^2+1}}$$

This integrand is discontinuous over the reals, yet it is possible to find an antiderivative, $G(x)$ (generated by Rubi), whose discontinuities occur in the same locations (at $x=-1$ and $x=1$):

$$G(x)=\frac{\tanh ^{-1}\left(\frac{\sqrt{3} x}{\sqrt{x^4+x^2+1}}\right)}{\sqrt{3}}$$

Now, by contrast, consider the integrand:

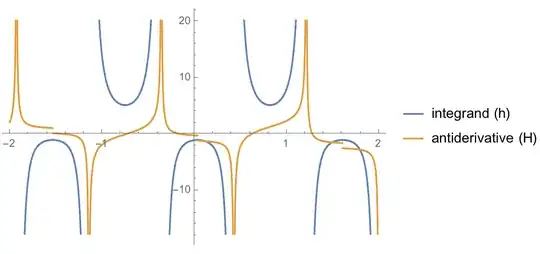
$$h(x)=\frac{(2 \sec (4 x+3)+1)^{3/2}}{\sqrt{\cos (4 x+3)}}$$

for which Rubi generates the following antiderivative (MMA's antiderivative is not real-valued on the reals); I believe $F$, $E$, and $\Pi$ are incomplete elliptic integrals of the first, second, and third kind, respectively:

Unlike the case with $G(x)$, $H(x)$ has discontinuities on the reals not present in its integrand (e.g., at $x = \frac{(\pi -3)}{4}$):

Given the above, should there exist another real-valued antiderivative of $h$ that, at least on the reals, has discontinuities that correspond to those of $h$?

I also have the following auxiliary question:

The quote from the WRI blog author mentions "simple poles". But I'm concerned with discontinuities generally, i.e., with anything that would require a piecewise integration. Thus I'm wondering if his statement can be generalized/reworded to something like: "If an integrand has one or more discontinuities, it is impossible to choose a single antiderivative that will be continuous everywhere."

Answer 1

By the Fundamental Theorem of Calculus, if the integrand $f(x)$ is continuous on an interval $(a,b)$, there is a continuous antiderivative on that interval, e.g. $\int_c^x f(t)\; dt$ where $a < c < b$. Finding an expression for it in a CAS is another matter.

It is possible for a discontinuous function $f(x)$ to have a continuous antiderivative. For example, consider $$f(x) = \cases{2x \sin(1/x) - \cos(1/x) & for $x \ne 0$\cr 0 & for $x=0$} $$ which has antiderivative $$ F(x) = \cases{x^2 \sin(1/x) & for $x \ne 0$\cr 0 & for $x=0$\cr}$$

EDIT: My first paragraph says you can avoid antiderivatives whose "discontinuity locations don't match the integrand's". Maybe it will help to look at your example $$\frac{(2 \sec(4x+3)+1)^{3/2}}{\sqrt{\cos(4x+3)}}$$ which, with the change of variables $4x+3=t$, becomes $$ \frac{(2 \sec(t)+1)^{3/2}}{\sqrt{\cos(t)}}$$ That is continuous on each interval of the form $((2k-1)\pi/2, (2k+1)\pi/2)$. Therefore it must have a continuous antiderivative on each of these intervals (as I wrote, finding a closed form for such an antiderivative is another matter). Since the integrand is undefined at the odd multiples of $\pi/2$ where $\cos(t) = 0$, the antiderivative doesn't have to be defined there either, and since the integrand has a non-integrable singularity there the antiderivative will also go to $\pm \infty$ as $t$ approaches those points.