Find $f$ such that $f^{-1}(\lbrace0\rbrace)$ is this knotted curve (M.W.Hirsh)

Question

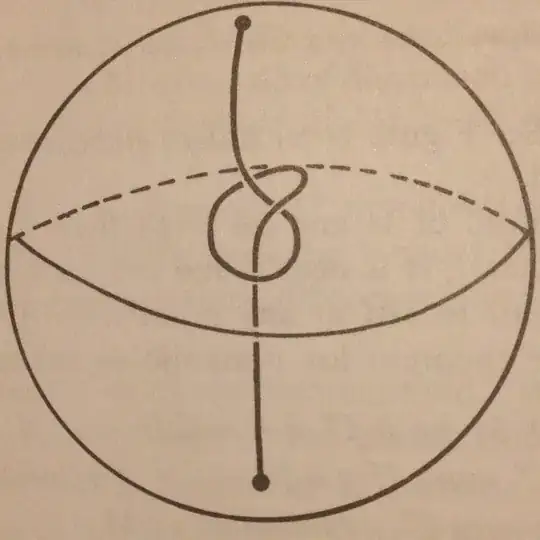
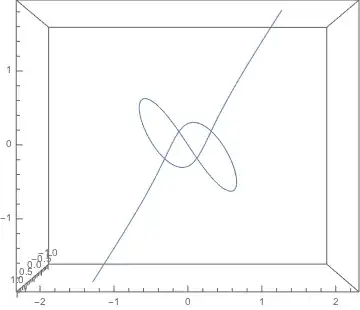
I would like to solve the following problem (it comes from Morris W. Hirsh, Differential Topology, it's exercise 6 section 4 chapter 1):

Show that there is a $C^\infty$ map $f:D^3\to D^2$ with $0\in D^2$ as a regular value such that $f^{-1}(\lbrace0\rbrace)$ is a knotted curve (as in the picture below).

I have been thinking about this problem for a while but I still have no answer. Here is what I came up with so far: if there was no knot on the figure and we wanted $f^{-1}(\lbrace0\rbrace)$ to be a straight line from north to south pole, then $f$ exists, we can take $f$ to be the orthogonal projection onto $(z=0)$. If we do so, we could precompose $f$ by a diffeomorphism of $D^3$ taking the straight line to the knot on the figure, which would give the answer. But I am pretty sure that such a diffeomorphism doesn't exists (the fundamental group of the complement of both path are not isomorphic), and it would be what makes this exercise difficult.

I've been thinking about moving the path to get a better viewpoint, but it didn't succeed.

I am really intrigued by this question, I like it a lot because it doesn't seem right. I am not looking for a complete answer (yet), I just would like a hint to feel how somebody should approach this problem. Thanks in advance for your help.

---

Edit: As suggested by Laz in the comments, there might be an answer to this problem involving techniques such as in this post. The idea would be to construct $f$ with polynomial coefficients. I went back to read the introduction of the book and this is what M.W.Hirsh says: "The more challenging exercises are starred, as are those requiring algebraic topology or other advanced topics." (This is a one star exercise).

So maybe M.W.Hirsh thought about a solution involving polynomial equations etc, but I must admit I would be a bit disappointed in this case, I was hoping that there is a solution involving differential topology. For example I had the following idea: take a tubular neighborhood of the curve $K$, which looks like $I\times D^2$, and define $f$ on this neighborhood by the projection of the second factor. We could try to extend $f$ on $D^3$ (but I don't see how).

Anyway at that point any kind of answer (involving differential topology or not) would be greatly appreciated.

---

Edit 2: Many thanks to HerrWarum for the bounty.

Answer 1

An alternate, algebraic approach: Let $S^3$ be the sphere $|z_1|^2+|z_2|^2=2$ in $\mathbb{C}^2$. Then the trefoil knot $K$ is given by the equation $z_1^3 = z_2^2$ in $S^3$, and can be parametrized as $(e^{2 i \theta}, e^{3 i \theta})$. Define $\phi: S^3 \to \mathbb{C}$ by $\phi(z_1, z_2) = z_1^3 - z_2^2$. So $K = \phi^{-1}(0)$.

I claim that $\phi$ is a submersion along $K$. If we consider $\phi$ as a map $\mathbb{C}^2 \to \mathbb{C}$, it is a submersion everywhere except at $(0,0)$. To verify that it is still a submersion when restricted to $S^3$, we must check that the $2$-dimensional kernel of $D \phi$ is transverse to the $3$-dimensional tangent space to $S^3$ at every point of $K$. To do this, I just have to give an element of $\mathrm{Ker}(D \phi)$ which is not in $TS^3$. Namely, at the point $(e^{2 i \theta}, e^{3 i \theta})$, the vector $(2 e^{2 i \theta}, 3 e^{3 i \theta})$ is in $\mathrm{Ker}(D \phi)$ but not in $TS^3$. (We can think of this vector as the derivative of $(e^{2 (t+i \theta)}, e^{3 (t+i \theta)})$ with respect to $t$. This curve lies on $z_1^3=z_2^2$, so its derivative is in $\mathrm{Ker}(D \phi)$, but it is clearly transverse to $S^3$.)

So we have a $C^{\infty}$ map from $S^3$ to $\mathbb{C}$ where $\phi^{-1}(0)=K$ and $\phi$ is a submersion along $K$. To convert to a map $\mathbb{R}^3 \longrightarrow \mathbb{R}^2$, just remove a point from $S^3$: Remove a point on $K$ to make a knot which stretches off to infinity as in the diagram, or remove a point not on $K$ to make a closed knot.

Here is a picture of your knot, in stereographic projection from the point $(1,1) \in S^3$:

It can be given parametrically as $$\left( \frac{\cos (2 t)-\cos (3 t)}{-\cos (2 t)-\cos (3 t)+2}, \ \frac{\sin (2 t)}{-\cos (2 t)-\cos (3 t)+2},\ \frac{\sin (3 t)}{-\cos (2 t)-\cos (3 t)+2}\right )$$

I get that the explicit coordinates of $\phi(u,v,w)$ are given by $$\begin{multline} \frac{1}{(1 + u^2 + 2 v^2 + 2 w^2)^3} \\ \left(-2 + 2 u - 12 u^2 - 4 u^3 + 6 u^4 + 10 u^5 + 56 v^2 - 120 u v^2 - 40 u^2 v^2 + 40 u^3 v^2 - 104 v^4 + 40 u v^4 + 24 w^2 - 24 u w^2 + 24 u^2 w^2 + 40 u^3 w^2 - 80 v^2 w^2 + 80 u v^2 w^2 + 24 w^4 + 40 u w^4, \right. \\ \left. 12 v - 48 u v + 24 u^2 v + 48 u^3 v + 12 u^4 v - 112 v^3 + 96 u v^3 + 48 u^2 v^3 + 48 v^5 + 8 w + 16 u w + 16 u^3 w - 8 u^4 w + 32 u v^2 w - 32 u^2 v^2 w - 32 v^4 w - 48 v w^2 + 96 u v w^2 + 48 u^2 v w^2 + 96 v^3 w^2 + 32 u w^3 - 32 u^2 w^3 - 64 v^2 w^3 + 48 v w^4 - 32 w^5 \right) \end{multline}$$ I got this by composing the inverse of sterographic projection, $$\frac{1}{1+u^2+2 v^2+2 w^2} \left(u^2+2 u+2 v^2+2 w^2-1,4 v,u^2-2 u+2 v^2+2 w^2-1,4 w\right)$$ and the map $z_1^3 - z_2^2$.

Answer 2

Main construction

Let $\gamma$ be the trefoil knot in $\mathbb{S}^3$. Since $\gamma$ is a fibered knot (see D. Rolfsen, Knots and Links, Chapters H and I), there is a tubular neighborhood $N\gamma \simeq \mathbb{S}^1\times\mathbb{D}^2$ and a fibration $f': \mathbb{S}^3\backslash\langle\gamma\rangle \rightarrow \mathbb{S}^{1}$ such that $$ f'(x,y) = \frac{y}{|y|}\quad\text{for all } (x,y)\in \mathbb{S}^1\times (\mathbb{D}^2\backslash\{0\}). $$ The projection to the second factor of $\mathbb{S}^1\times\mathbb{D}^2$ determines a smooth map $f'': N\gamma \rightarrow \mathbb{D}^2$ with regular value $0$ and with $(f'')^{-1}(0)=\langle\gamma\rangle$. We define $f: \mathbb{S}^3 \rightarrow \mathbb{D}^2$ by $$f(z):=\begin{cases} f''(z) &\text{for }z\in N\gamma, \text{ and by}\\ f'(z) & \text{otherwise}. \end{cases}$$ The compatibility condition guarantees that $f$ is continuous. Notice that the entire complement of $N\gamma$ gets mapped into $\mathbb{S}^1 = \partial \mathbb{D}^2$.

Some details

1) Looking at the figure, we extend the curve through the boundary points outside of $\mathbb{D}^3$ and connect the two ends there to obtain the trefoil $\gamma: \mathbb{S}^1 \rightarrow \mathbb{R}^3$. We then pick a smooth embedding $\psi: \mathbb{R}^3\rightarrow \mathbb{S}^3$, transfer everything to $\mathbb{S}^3$, and construct $f: \mathbb{S}^3 \rightarrow \mathbb{D}^2$. In the end, we consider the restriction $f\circ \psi: \mathbb{D}^3 \rightarrow \mathbb{D}^2$.

2) The main construction gives a continuous extension $f: \mathbb{S}^3 \rightarrow \mathbb{D}^2 \subset \mathbb{R}^2$ of the smooth map $f'': N\gamma \rightarrow \mathbb{D}^2$ such that $f(\mathbb{S}^3 \backslash N\gamma)\subset \mathbb{S}^1$. To make $f$ smooth, we apply Theorem 2.5 from Chapter I of A. Kosinski, Differentiable manifolds:

Theorem 2.5: Let $f:M\rightarrow \mathbb{R}^n$ be a continuous map, smooth on a closed subset $K$ of $M$, and let $\varepsilon>0$. Then there is a smooth map $g: M \rightarrow \mathbb{R}^n$ that agrees with $f$ on $K$ and such that $|f(p) - g(p)| < \varepsilon$ for all $p\in M$.

Applying this theorem to $f$, $M=\mathbb{S}^3$, $K=\frac{3}{4}N\gamma$, $n=2$ and $\varepsilon = \frac{1}{2}$, we obtain a smooth map $g: \mathbb{S}^3 \rightarrow \mathbb{R}^2$ which equals $f$ on $K$ and such that $g^{-1}(0) = f^{-1}(0)$. Since $\mathbb{S}^3$ is compact, we can scale $g$ by a constant to achieve $g(\mathbb{S}^3)\subset \mathbb{D}^2$. The scaling changes neither the regularity of $0$ nor the level set $g^{-1}(0)$. This $g$, after the procedures from 1), is then the map $f$ we have been looking for.

Acknowledgment

The problem was solved with the help of Prof. Dr. Urs Frauenfelder who suggested to look in the Rolfsen's book for the precise definition of a fibered knot.

Reaction to comments:

@Moishe Kohan: It seems like that you are using a more general definition of a fibered knot where the compatibility condition does not necessarily hold, e.g., the definition from J. Harer, How to construct all fibered knots. This definition requires only that the complement $W:=M\backslash K$, where $M$ is a $3$-manifold and $K$ the knot, is a fibration over $\mathbb{S}^1$ such that closures of its fibers $F$ are Seifert surfaces. We then have $W\simeq F \times [0,1]/\sim$, where the ends are identified by a general homeomorphism $h$ of $F$. Then, of course, the intersection $F \cap N\gamma$, which is a knot itself, might link with $K$ non-trivially, depending on $h$.

However, the definition of a fibred knot from the Rolfsen's book, which I am using, imposes the compatibility condition, and hence link $link(F\cap N\gamma, K)=0$. This is a screenshot from the Rolfsen's book:

A fibration of the trefoil satisfying this definition is constructed explicitly in Chapter I of the book.

According to your terminology, a fibration satisfying $link(F\cap N\gamma, K)=0$ is called a Seifert fibration. Hence, it seems like that Rolfsen defines and works with Seifert fibrations implicitly.

To complete the reply to your comment, I sum up the issue of the regular value here:

It holds $f^{-1}(0)=(f'')^{-1}(0)=\langle\gamma\rangle$ because the image of $f'$ lies inside of $\mathbb{S}^1$. Also, $0$ is a regular value of $f''$ since $f''$ is just a projection to the second component. It is also a regular value of $f$ as it agrees with $f''$ on a neighborhood of $\langle\gamma\rangle$. The smoothening of $f$ does not change these facts.