Find function $f(x)$ satisfying $\int_{0}^{\infty} \frac{f(x)}{1+e^{nx}}dx=0$

Question

I am looking for a non-trivial function $f(x)\in L_2(0,\infty)$ independent of the parameter $n$ (a natural number) satisfying the following integral equation: $$\displaystyle\int_{0}^{\infty} \frac{f(x)}{1+e^{nx}}dx=0$$ or prove that $f(x)=0$ is the only solution.

The similar question is here but there are no parameters in the integral and the answer is based upon hit and trial method.

I want to know what would be the nice approach to tackle this problem.

EDIT: Such a function may exist, here is an example due to Stieltjes. A function $f(x) = \exp(-x^{1/4}) \sin x^{1/4}$ satisfies $\int_0^{\infty} f(x) x^n dx = 0$ for all integers $n \ge 0$.

We use the substitution $x=u^4$ to write $I_n = \int_0^{\infty} f(x) x^n dx = 4 \int_0^{\infty} e^{-u} \sin(u) u^{4n+3} du$; then integrate by parts four times (differentiating the power of $u$, and integrating the rest) to show that $I_n$ is proportional to $I_{n-1}$, and finally check that $I_0=0$.(the Edit copied from here)

Answer 1

I'll prove a partial result that hopefully someone can complete to showing that $f(x) \equiv 0$ is the unique continuous and $L^2(\mathbb{R}_{>0})$ solution. Beyond that, perhaps one can use that continuous functions are dense in $L^2$ to get the requested result. The main tool I want to contribute is the following lemma:

$\mathbf{Lemma}:$ Consider $f \in C(\mathbb{R}_{>0}) \cap L^2(\mathbb{R}_{>0})$. Then for any choice of $0<x_0<y_0 \leq \infty$, we have

$$f(x_0) = \lim_{n \to \infty} ne^{nx_0}\int_{x_0}^{y_0}\frac{f(x)}{1+e^{nx}}dx $$

$\mathbf{Proof}:$ Fix $\epsilon>0$ and, by continuity, choose $\delta>0$ such that $|x-x_0| < \delta \implies|f(x)-f(x_0)| < \epsilon$. Note that

$$\lim_{n \to \infty} ne^{nx_0} \int_{x_0}^{x_0+\delta} \frac{1}{1+e^{nx}}dx = 1$$

and

\begin{align} \lim_{n \to \infty} \left | n e^{nx_0} \int_{x_0+\delta}^{y_0}\frac{f(x)}{1+e^{nx}} dx \right | & \leq \lim_{n \to \infty} n e^{nx_0} \int_{x_0+\delta}^{y_0} e^{-nx} |f(x)| dx \\ & \leq \lim_{n \to \infty} n e^{nx_0} e^{-(n-1)(x_0+\delta)} \int_{x_0+\delta}^{y_0} e^{-x} |f(x)| dx \\ & \leq \lim_{n \to \infty} n e^{x_0+\delta} e^{-n\delta} \|e^{-x}f(x)\|_1 \\ & \leq \lim_{n \to \infty} n e^{x_0+\delta} e^{-n\delta} \|e^{-x}\|_2 \cdot \|f\|_2 \\ & = 0 \end{align}

by Holder's inequality (neither of these depended on the choice of $\delta$-- they're just straightforward computation/comparison). Given these results, we see that

\begin{align} \lim_{n \to \infty} \left |ne^{nx_0} \int_{x_0}^{y_0} \frac{f(x)}{1+e^{nx}}dx - f(x_0) \right | & = \lim_{n \to \infty} \left |ne^{nx_0} \int_{x_0}^{x_0+\delta} \frac{f(x)-f(x_0)}{1+e^{nx}}dx \right | \\ & \leq \lim_{n \to \infty} ne^{nx_0} \int_{x_0}^{x_0+\delta} \frac{|f(x)-f(x_0)|}{1+e^{nx}}dx \\ & \leq \epsilon \end{align}

Since $\epsilon>0$ was arbitrary, this proves the lemma. $$\tag*{$\blacksquare$}$$

This lemma gives us some insight into the behavior of functions satisfying your condition. In particular, if $f$ satisfies these hypotheses and the condition under consideration, we must have for any $x_0 > 0$ that

$$0 = \lim_{n \to \infty} ne^{nx_0} \int_{0}^\infty \frac{f(x)}{1+e^{nx}}dx = f(x_0) + \lim_{n \to \infty} ne^{nx_0} \int_{0}^{x_0} \frac{f(x)}{1+e^{nx}}dx$$ Or

$$f(x_0) = -\lim_{n \to \infty} ne^{nx_0} \int_0^{x_0} \frac{f(x)}{1+e^{nx}}dx $$

From this result, we have $\forall$ $0<x_0<y_0<\infty$ that

$$\lim_{n \to \infty} ne^{nx_0} \int_0^{y_0} \frac{f(x)}{1+e^{nx}}dx = \lim_{n \to \infty} e^{-n(y_0-x_0)} \left [ ne^{ny_0} \int_0^{y_0} \frac{f(x)}{1+e^{nx}}dx \right ] = 0 \cdot (-f(y_0)) = 0 $$

and similarly $\forall$ $0 < w_0 < x_0$ with $f(w_0) \neq 0$, the expression

$$ne^{nx_0} \int_0^{w_0} \frac{f(x)}{1+e^{nx}}dx = e^{n(x_0-w_0)} \left [ ne^{nw_0} \int_0^{w_0} \frac{f(x)}{1+e^{nx}}dx \right ] $$ diverges to $-\text{sgn}(f(w_0)) \cdot \infty$ as $n \to \infty$, since the term in brackets approaches $-f(w_0)$.

Now, suppose $f$ is not identically $0$, so the set

$$\{t >0 | f \equiv 0 \text{ on } (0,t) \}$$

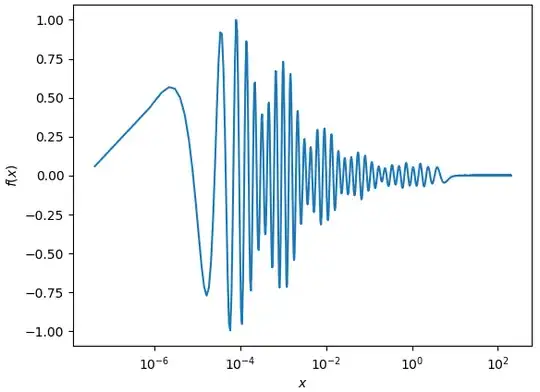
is bounded above; define $T_1$ as the supremum of this set if it is nonempty and $0$ if it is empty. Suppose $\exists T_2>T_1$ such that $$ T_1 < t < T_2 \implies f(t) \neq 0$$ Then $f$ is nonzero on $(T_1,T_2)$ by definition, so by the Intermediate Value Theorem $f$ cannot change sign in this interval. Thus either $f(x) \geq 0$ or $-f(x) \geq 0$ on $(0,T_2)$-- WLOG assume the former, so that for any $x_0 \in (T_1,T_2)$ the first identity after the lemma gives that $f(x_0) \leq 0$, showing $f(x_0)=0$, a contradiction. We therefore conclude that no such $T_2$ exists, i.e. $\forall t>T_1$ $\exists s \in (T_1,t)$ such that $f(s)=0$. That is to say, on any interval containing $0$ on which $f$ is not identically zero, $f$ must have infinitely many roots greater than $T_1$. In particular, the suggestion $f(x)=e^{-x^{1/4}} \sin(x^{1/4})$ cannot be a solution.

Note that if one can use the above results to show that $T_1 = 0$, it would establish that no continuous solution with compact support on $\mathbb{R}_{>0}$ exists (relevant because such functions are dense in $L^2(\mathbb{R}_{>0})$).

Answer 2

The only such function is $f\equiv 0$. The proof is fairly standard but if you've never seen such machinery before, it may take some time and effort to comprehend, so feel free to ask questions if something is unclear.

Lemma: If $f$ satisfies the condition, then $F(z)=\int_{0}^\infty \frac{f(x)}{1+e^{zx}}dx=0$ for all real $z>0$. Proof: $F$ is analytic in the right half-plane $\Re z>0$ and, moreover, grows at most polynomially in $\Re z>1$, say. Thus $z^{-N}F(z)$ is a bounded analytic function in $\Re z>1$. By hypothesis, $F$ has zeroes at all integer points, and $F$ must vanish identically (the Blaschke condition is violated). This proves the lemma.

By the lemma, if $f$ satisfies the condition, then $\int f(x)K_t(x)dx=0$ for all $t$, where $K_t(x)=\frac 1{1+e^{tx}}$. So the main result will follow from the density of the family $K_t$ in $L^2(0,+\infty)$. This the same as the density of the family $k_t$ in $L^2((0,+\infty),\frac{dx}{x})$ where $k_t(x)=\frac{\sqrt{tx}}{1+e^{tx}}$. Up to a logarithmic change of variable, this is also the same as the problem about completeness of shifts in $L^2(\mathbb R)$. The answer is given by the Wiener criterion: the family is dense if the Fourier transform of the generating function vanishes only on a set of measure $0$. So the family is dense if the transform $$ \int_0^\infty \frac{\sqrt x}{1+e^x}x^{-is}\,\frac{dx}x\ne 0 $$ for almost all $s\in\mathbb R$. But the left hand side is analytic in $s$ for $|\Im s|<\frac 12$, and not identically zero, so the real zeroes of the transform are at most a discrete set, and the transforms are non-zero for almost all $s$. QED

Answer 3

Edit: Assuming a non-zero $f(x)$ exists - if it is antisymmetric about $x=0$ and can be expressed by a Fourier integral $$f(x) = \int_{-\infty}^\infty F(\omega) \sin(\omega x) {\rm d}\omega ,$$ it can be shown that $$\lim_{n\rightarrow\infty}\int_0^\infty \frac{f(x)}{1+\exp(nx)}{\rm d}x = 0 :$$

for all spectral components of the assumed antisymmetric $f(x)$ proportional to $\sin(\omega x)$, the integral $$\int_0^\infty \frac{\sin(\omega x)}{1+\exp(nx)}{\rm d}x = \frac{n\sinh(\frac{\pi\omega}{n})-\pi\omega}{2n\omega\sinh(\frac{\pi\omega}{n})}$$ vanishes for $n\rightarrow\infty$ (and also for $\omega\rightarrow\infty$ since $n$ is non-zero).

And here the previous attempt at a numerical solution...
The approximate $f(x)$ in the plot below was constructed by numerically integrating $f(x)/(1+\exp(nx))$ and considering all $n$ up till including $30000$ and sampling $f(x)$ on a logarithmic-like grid with $15000$ points. $f(x)$ appears to consist of a superposition of functions of the form $\sin({\rm const} + \log({\rm const}_1+{\rm const}_2\cdot{}x))$, but it's hard to deduce a closed form...

The fact that this numerical solution stops oscillating at $x\sim10$ likely is an artifact of limited numerical precision; due to $(1+\exp(nx))^{-1}$ in the kernel, there is very little weight on $f(x)$ at larger $x$ and it is hard to obtain more precise values for $f(x)$.
For large $n$, which should have a dominating influence on $f(x)$ for $x\rightarrow 0$, the finite number of grid points limits the qualitity of the solution for $f(x)$. For sufficiently large $n$ and with a finite number of grid points, $f(x\rightarrow 0)\rightarrow 0$ will be sufficient to satisfy the numerical solution attempted here.

Here is the Python code used to generate the figure above:

#number of grid points
N = 15000
#max n considered (can be/should be larger than N for least-squares
#solution below)
n = 2*N

#external dependencies
import numpy as np
from numpy.polynomial.legendre import leggauss

#create quadrature roots and weights
#beginning with interval [-1;1]
xp,wp = leggauss(N)
xp *= 0.5
xp += 0.5
#rescale to 0..infinity
scale = 6.0
x = np.sinh(scale*xp)
w = wp * scale/2. * np.cosh(scale*xp)

#create system of equations: Integral(n) = 0, n=0...
#we also constrain Int(0) = 0 (although only n=1... required) ...
#... seems to be more stable numerically (otherwise almost no weight on
#f-values at large x)
A = []
for i in range(n+1):
    A.append(np.empty_like(x))
    for j in range(len(x)):
        if x[j]*i<500.:
            A[-1][j] = w[j]/(1.+np.exp(x[j]*i))
        else:
            A[-1][j] = 0.0

#add additional for f at x approx 0.5 to avoid trivial solution f=0
#(hoping to not accidentally hit a root of f(x))
z = np.zeros_like(x)
z[np.argmin(np.abs(x-0.5))] = 1.
A.append(w)

A = np.array(A)

#RHS of system of equations
b = np.concatenate((np.zeros(n+1,np.float),[1.]))

#least-squares solution for f(x)
sol = np.linalg.lstsq(A,b,rcond=1e-14)[0]
#normalize
if -np.min(sol)>np.max(sol):
    sol *= -1.0
sol /= np.max(sol)

#plot solution
import pylab
pylab.plot(x,sol)
pylab.xscale('log')
pylab.xlabel('$x$')
pylab.ylabel('$f(x)$')
pylab.show()

Answer 4

The linearized version has a nice solution. If we use a Taylor series at $x=0$ to approximate $$\frac{1}{1+e^{nx}}\ \simeq\ \max\left(\frac{1}{2} - \frac{nx}{4},\ 0\right)$$ then the linearized problem asks for a non-trivial $f$ in $L^2$ with $$\int_0^{2/n}\left(\frac{1}{2} - \frac{nx}{4}\right)f(x)dx = 0$$ valid for all $n$.

Let $$ f_m(x)= \begin{cases} +1\ \ \text{ if }\ \ x \in (\frac2{m+1}, \phantom{+ 3a_m},\ \frac2{m+1} + \phantom{3}a_m)\\ -1\ \ \text{ if }\ \ x \in (\frac2{m+1} + \phantom{3}a_m, \ \frac2{m+1} + 3a_m),\text{ where }a_m=\dfrac{1}{2m(m+1)}\\ +1\ \ \text{ if }\ \ x \in (\frac2{m+1} + 3a_m, \ \frac2{m+1} + 4a_m)\\ \ \ 0 \ \ \ \ \text{otherwise.} \end{cases} $$ $\ \ $

Each $f_m$ is non-zero on the interval $(2/(m+1), 2/m)$. Furthermore the product of $f_m$ with any linear function has an integral of $0$, because the middle half of a trapezoid has the same area as the two outer quarters.

So $$f=\sum_{m=1}^\infty f_m$$ is an $L^2$ function, alternating between $+1$ and $-1$, with a square-integral of $2$, which solves the linearized problem.

For the original problem, we could try a similar technique by dividing the interval $(2/(m+1), 2/m)$ into $m$ different subintervals so that all of the relevant integrals are $0$.

Alternatively, any proof that the original problem has no solution will have to use some surprisingly detailed properties of $1/(1+e^{nx})$.

Answer 5

The issue condition can be written in the form of $$\int_0^\infty f\left(\dfrac zn\right)\dfrac{dz}{1+e^z} = 0.\tag1$$ Let the Maclaurin series of $f(x)$ exists, then $$f(z) = \sum\limits_{k=0}^\infty a_kz^k.$$

Taking in account the integral representation of the Riemann zeta function in the form of

$$\int\limits_0^\infty\dfrac {z^k\,dz}{1+e^z} = (1-2^{-k})k!\zeta(k+1)\tag3$$

(see also Wolfram Alpha),

one can get $$I_n = \sum\limits_{k=0}^\infty \dfrac{a_k}{n^k} \int\limits_0^\infty\dfrac {z^k\,dz}{1+e^z} = \sum\limits_{k=0}^\infty \dfrac{1-2^{-k}}{n^k}k!\zeta(k+1) = 0,$$ $$I_n = \sum\limits_{k=0}^\infty \dfrac{b_k}{n^k} = 0\quad \forall (n\in \mathbb N),\tag4$$ where $$b_k = (1-2^{-k})k!\zeta(k+1).\tag5$$ The system $(4)$ is linear relatively to the coefficients $b_k.$ On the other hand, determinant of this system is

$$ \Delta = \begin{vmatrix} 1 & 1 & 1 & 1 & 1 & \dots & 1 & \dots \\ 1 & \dfrac12 & \dfrac1{2^2} & \dfrac1{2^3} & \dfrac1{2^4} & \dots & \dfrac1{2^k} &\dots\\ 1 & \dfrac13 & \dfrac1{3^2} & \dfrac1{3^3} & \dfrac1{3^4} & \dots & \dfrac1{3^k} &\dots\\ 1 & \dfrac14 & \dfrac1{4^2} & \dfrac1{4^3} & \dfrac1{4^4} & \dots & \dfrac1{4^k} &\dots\\ &&&&\dots\\ 1 & \dfrac1n & \dfrac1{n^2} & \dfrac1{n^3} & \dfrac1{n^4} & \dots & \dfrac1{n^k} &\dots\\ \end{vmatrix}\\[6pt] = \begin{vmatrix} 1 & 1 & 1 & 1 & 1 & \dots & 1 & \dots \\ 0 & -\dfrac12 & -\dfrac1{2^2} & -\dfrac1{2^3} & -\dfrac1{2^4} & \dots & -\dfrac1{2^k} &\dots\\ 1 & -\dfrac23 & -\dfrac2{3^2} & \dfrac2{3^3} & \dfrac2{3^4} & \dots & -\dfrac2{3^k} &\dots\\ 1 & -\dfrac34 & \dfrac3{4^2} & -\dfrac3{4^3} & -\dfrac3{4^4} & \dots & -\dfrac3{4^k} &\dots\\ &&&&\dots\\ 1 & -\dfrac{n-1}n & -\dfrac{n-1}{n^2} & -\dfrac{n-1}{n^3} & -\dfrac{n-1}{n^4} & \dots & \dfrac1{n^k} &\dots\\ \end{vmatrix}\\[6pt] \sim \begin{vmatrix} 1 & 1 & 1 & 1 & 1 & \dots & 1 & \dots \\ 0 & 1 & \dfrac12 & \dfrac1{2^2} & \dfrac1{2^3} & \dots & \dfrac1{2^k} &\dots\\ 0 & 1 & \dfrac13 & \dfrac1{3^2} & \dfrac1{3^3} & \dots & \dfrac1{3^k} &\dots\\ 0 & 1 & \dfrac14 & \dfrac1{4^2} & \dfrac1{4^3} & \dots & \dfrac1{4^k} &\dots\\ &&&&\dots\\ 0 & 1 & \dfrac1n & \dfrac1{n^2} & \dfrac1{n^3} & \dots & \dfrac1{n^k} &\dots\\ \end{vmatrix} \not = 0.$$

If the homogenius linear system has unzero determinant, then zero solution is single.

Looks that consideration of the determinant sequences allows to assume that $\textbf{the issue task has only the trivial solution}$.

Answer 6

There is no one continuous function that will satisfy that for all n.

By trivial solution I assume you mean $f(x)=0$. One potential (although also fairly trivial, or at least boring) answer is

$$f(x)=(1+e^{nx})g(x)$$

where

$$\int_0^{\infty} g(x) \, dx=0$$

say maybe $\sin(x)$ or indeed any periodic function that acts in this way. However, this of course is not strictly defined as our $\epsilon-\delta$ definition will not hold for convergence, i.e.

$$\lim_{x\to\infty} \int_0^n \sin(x) \, dx$$

is not defined, so that is not an option either.

Let us now consider to look at this graphically. Imagine, if you can, the graph of such a function, say defined from $0$ to $\infty$ such that our integral is zero. Without a loss of generality, let us say that this function is positive to start with, so at some point, say $x_0$ this function will have to cross the $x$ axis and become negative.

This means that our function has to be periodic and increasing at exactly the same rate and time as $1+e^{nx}$, thus resulting in only the trivial solution as above, or that the finitely bounded area before this critical value $x_0$ has identical area to our unbounded area beyond $x_0$.

This means that our function $f(x)$ satisfies $$\int_0^{x_0}f(x) \, dx=-\int_{x_0}^\infty f(x) \, dx$$

As the function must satisfy this for all n this answer should suffice to show that the function $f(x)$ must be trivial, as if $f(x)$ satisfies this for some n, the the denominator will grow at a different rate for a different n, thus showing that there is no such $f(x)$.