0

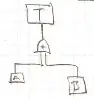
I made this statement $P(T|A)=P(T|B)=0=P(T|\neg A)=P(T|\neg B)$ with a simple OR-gate where $P(A)=0$, $P(B)=0$ and $T=A\cdot B$ i.e. $P(T)=P(A\cup B)$.

enter image description here

What are the conditional probabilities of the system i.e. $P(T|A)$, $P(T|\neg A)$, $P(T|B)$ and $P(T|\neg B)$?

hhh
  • 5,605

1 Answers1

1

Suppose A works, what is the probability that the system works i.e. $P(T|A)$? Look A has 0% working probability i.e. $P(A)=0$ so what does the phrase "A works" mean here? The term "working" can mean at least two things: $P(A)=1$ or $P(A)>0$. The latter requires thinking probabilities with intervals.

The below threads address the aroused issues so far.

Sub-problems

  1. Solved $P(T\cap \neg B)$ if $P(T)=P(A\cup B)$ where $P(A)=0$ and $P(B)=0$?

  2. Solved Complement and Negation: $P(A)=0\rightarrow P(\neg A)=1$?

  3. Conditional probabilties in the OR-gate $T=A\cdot B$ with zero-probabilities in $A$ and $B$?

Community
  • 1
hhh
  • 5,605