3

Let G be a bipartite graph all of whose vertices have the same degree d. Show that there are at least d distinct perfect matchings in G. (Two perfect matchings M1 and M2 are distinct if M1 does not equal to M2 as sets.)

I am probably not understanding the definition of distinct perfect matching correctly. For example, if we have a regular bipartite graph with d = 2 like the one below:

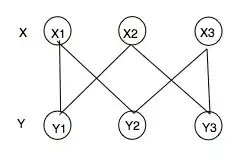
enter image description here

It says M1 and M2 are different if they are different "as sets". Say we are looking at the perfect matching of X, or does it mean sets of edges or sets of vertices?

If it's sets of vertices, it can be {Y1, Y2}, {Y2, Y3} and {Y1, Y2, Y3}.

If it's sets of edges there are apparently 2 x 2 x 2 = 6 different sets.

And besides these, I have no clue how to attack this problem anyway, regardless of what it meant by "sets"...

I thought the answer would be d^(d/2) which is way off and absolutely wrong...

Help with intuitive explanation and steps are appreciated!!!

Angus Leo
  • 119

1 Answers1

2

Hint:

  • It is trivial for $d = 1$.
  • For $d > 1$, remove edges of any perfect matching to get $(d-1)$-regular bipartite graph with $(d-1)$ distinct perfect matchings.

Good luck!

dtldarek
  • 37,969
  • This gives matchings that are not just distinct but disjoint! But you do have to say why there is even one perfect matching. – Gerry Myerson Feb 25 '13 at 12:17
  • I don't see how you can always "remove edges of any perfect matching to get (d−1)-regular bipartite graph with (d−1) distinct perfect matchings." How? Is it possible that such removal cannot be done? Let's say we start removing one edge from each vertex from the side that has a perfect matching into the other side. What if 2 edges got removed connect with the same vertex on the other side and that vertex cannot maintain a d-1 degree??? – Angus Leo Feb 25 '13 at 12:51
  • 1
    @GerryMyerson Because of Hall's theorem. – dtldarek Feb 25 '13 at 13:15
  • @AngusLeo You didn't provide any context for your question, so all I can provide is a hint. BTW, if $\geq 2$ edges connect the same vertex on the other side, would that be a matching? – dtldarek Feb 25 '13 at 13:21
  • Never mind, I have figured it out. Thanks! :) – Angus Leo Feb 25 '13 at 14:02