Injectivity, surjectivity and pullback diagrams

Question

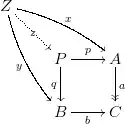
Consider the following pullback diagram (in any category):

$$ \newcommand{\ra}[1]{\kern-1.5ex\xrightarrow{\ \ #1\ \ }\phantom{}\kern-1.5ex} \newcommand{\ras}[1]{\kern-1.5ex\xrightarrow{\ \ \smash{#1}\ \ }\phantom{}\kern-1.5ex} \newcommand{\da}[1]{\bigg\downarrow\raise.5ex\rlap{\scriptstyle#1}} \begin{array}{c} A \times_C B & \ra{p} & A \\ \da{q} & & \da{a} \\ B & \ras{b} & C \\ \end{array} $$

with $a$ a monomorphism and $b$ an epimorphism. I would like to understand necessary and/or sufficient conditions for $p$ to be an epimorphism too.

The following might be relevant:

Lemma: $q$ is always a monomorphism (and dually, in all pushout diagrams, the same statement holds for the epimorphism)

Proof: Assume that we have two maps $u_1, u_2$ from some object $W$ to $A \times_C B$ such that $q \circ u_1 = q \circ u_2$. Then $a \circ p \circ u_1 = a \circ p \circ u_2$ because the diagram is Cartesian, and therefore $p \circ u_1 = p \circ u_2$ because $a$ in a monomorphism. But since $u_1$ and $u_2$ are uniquely determined by their compositions $p \circ u_i$ and $q \circ u_i$, and since both coincide, we have that $u_1 = u_2$, and therefore $q$ is a monomorphism. QED

I have read here a proof for Abelian categories, but I think that my proof should be ok for any category, am I wrong? Anyway, back to the main point:

Question: When is $p$ an epimorphism too?

I don't expect this to be always true. But maybe there are necessary and/or sufficient conditions for when this works. For instance, for Sets it is always true (just look at the explicit construction of the pullback).

PS: I have seen here that it is true in any Abelian category.

Answer 1

Yes, the statement about monomorphisms is true on any category. Your proof is correct.

As you said, the statement for epimorphisms is not always true. For example, in the category of Hausdorff topological spaces, let $b$ have dense image but not surjective (this is an epimorphism) and let $a$ have image contained in the complement of the image of $b$. Then the fiber product $A\times_{C}B$ is empty, so $p$ won't be an epimorphism unless $A$ was empty.

In abelian categories, pullbacks of epimorphisms are always epimorphisms. More generally, the notion you need is that of a regular category on which every epimorphism is regular (i.e. the coequalizer of some pair of morphisms). In a regular category, regular epimorphisms always pull back to regular epimorphisms by definition.

Besides abelian categories, the category of sets is also regular. Moreover, all epis of sets are regular. This explains your last remark about the category Set.

Answer 2

A simple condition in a category which make epimorphisms stable under pullback is the following:

In a category with a projective generator, epimorphisms are stable under pullback.

Recall that as object $Z$ is a generator if for each pair of distinct parallel morphisms $f,g:X\to Y$ there exists a morphisms $x:Z\to X$ such that $xf\neq xg$. An object $Z$ is projective if and only if for each epimorphism $e:X\to Y$ and each morphism $y:Z\to Y$ there exists a morphism $x:Z\to X$ such that $y=xe$.

This condition is fullfilled, for example:

• in the category of sets by taking $\{\varnothing\}$ as projective generator;
• in the cateogry of modules over a ring taking the ring itself as projective generator;
• in the category of groups taking $\Bbb Z$ as projective generator.

proof. The proof of this fact follows at once by noting that given a projective generator $Z$, a morphism $f:X\to Y$ is an epimorphisms if and only if for all $y:Z\to Y$ there exists $x:Z\to X$ such that $y=xf$.

The only if part is follows since $Z$ is projective. For the if part follows arguing by contradiction: if $f$ is not an epimorphism, then there exists a pair of distinct parallel arrows $u,v:Y\to W$ such that $fu=fv$.

Since $Z$ is a generator, there exists $y:Z\to Y$ such that $yu\neq yv$. Let $x:Z\to X$ such that $xf=y$. Then $$yu=xfu=xfv=yv$$ a contradiction.

Now consider the pullback square below. We claim that $q$ is epic. Let $y:Z\to B$. Then $yb:Z\to C$ and since $a$ is epic, there exists $x:Z\to A$ such that $yb=xa$. Since the square is a pullback, there exists $z:Z\to P$ such that $y=zq$.