Pattern of Newton-Raphson iteration $x\mapsto\frac{1}{2}(x+\frac{q}{x})$ over finite fields

Question

While playing with Newton-Raphson method over finite field $\mathbb{F}_p$, I noticed some cute patterns that I can't explain out of my brain contaminated with analysis.

Here is the setting:

Setting. Let $p$ be an odd prime and $q \in \mathbb{F}_p$. Define the directed graph $G_{p,q}$ as follows:

• The vertex-set of $G_{p,q}$ is simply $\mathbb{F}_p$.
• A (directed) edge $[x, y\rangle$ is in the edge-set of $G_{p,q}$ if and only if $x^2 - 2xy + q = 0$ holds.

In the case $q \neq 0$, edges of $G_{p,q}$ are of the form $[x, f(x) \rangle$ for $f(x) = \frac{1}{2}(x+\frac{q}{x})$ and $x\in\mathbb{F}_p\setminus\{0\}$. Notice that $f$ is the exactly the function which arises in the Newton-Raphson's method for finding zeros of $x^2 - q$.

Here is a quick observation: For each $ y \in \mathbb{F}_p$, either

1. $y^2-q$ is a non-zero quadratic residue modulo $p$, so that are exactly $2$ edges pointing at $y$.

2. $y^2 - q = 0$ in $\mathbb{F}_p$, so that $\{y\}$ is a connected component of $G_{p,q}$ with the loop $[y, y\rangle$.

3. $y^2 - q$ is not a quadratic residue modulo $p$, so that no edge points at $y$, i.e., $y$ is a leaf.

It seems that, for each given $p$, the connectivity structure of $G_{p,q}$ depends only on whether $q$ is a quadratic residue modulo $p$ or not. For instance, if $p=43$, then only the following two possibilities of connectivity emerge:

And the following is the case of $p=113$.

So the obvious question is

Question.

(1) Can we find an explanation as to why the connectivity structure of $G_{p,q}$ for $p$ odd prime and $q \in \mathbb{F}_{p}\setminus\{0\}$ seems to depend only on the quadratic residue of $q$?

(2) Can we relate any of the structure of $G_{p,q}$ in terms of number-theoretic properties of $(p, q)$? For instance, what is so special about this construction that components look so 'symmetric'?

I know that I am rather throwing random questions out of shallow curiosity, so forgive me if the questions look like not well-formed or it is already well-known. I would like to consider this question as a recreational one, and would appreciate any comment.

Answer 1

Assume first that $q$ is a quadratic residue modulo $p$. By Misha Lavrov's answer we can then assume that $q=1$. We are interested in the behavior of the iterates of $$ f(x):=\frac12\left(x+\frac1x\right). $$

Consider the Möbius transformation from the set $P=\Bbb{F}_p\cup\{\infty\}$ to itself $$ \mu(t):=\frac{t+1}{t-1}. $$ We see that $$ \begin{aligned} f(\mu(t))&=\frac12\left(\frac{t+1}{t-1}+\frac{t-1}{t+1}\right)\\ &=\frac{t^2+1}{t^2-1}\\ &=\mu(t^2). \end{aligned} $$ This means that, up to conjugation by $\mu$, the mapping $f$ is just squaring in the set $P$. Therefore $f$ and squaring produce isomorphic graphs of transitions.

What happens in the set $P$ when we iteratedly square elements was studied in this thread (apologies for blowing my own trumpet to this extent). Anyway, we can say the following:

Assume $q$ is a quadratic residue. Write $p-1=2^m a,$ where $a$ is odd. Then after $m$ iterations of $f$ the set of images has stabilized. Call this set $S$. Then further iterations will just permute the set $S$. The cycle structure of a single iteration on set $S$ can be gotten by looking at what happens with multiplication by two modulo $a$.

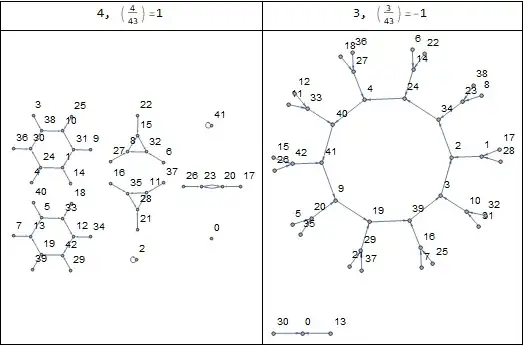
As an example let's consider the case $p=43$. This time $m=1, a=21$. Modulo $21$ multiplication by two produces the cycles $$ (0)(1,2,4,8,16,11)(3,6,12)(5,10,20,19,17,13)(7,14)(9,18,15). $$ Indeed, we see two 6-cycles, two 3-cycles and a single 2-cycle in Sangchul Lee's image of this graph.

On the other hand, with $p=113$ we get $p-1=2^4\cdot7$. This explains why we get the reverse of binary branching up to depth four, and then modulo $a=7$ we see the cycles $$ (0)(124)(365). $$

---

When $q$ is not a square of an element of $\Bbb{F}_p$ the situation is a little bit different. To apply the above ideas we also work inside the quadratic extension field $\Bbb{F}_p(\sqrt{q})$.

This time we are interested in the iterations of $$ f(x)=\frac12\left(x+\frac q x\right). $$ As above, we see that with (as observed by Sangchul Lee in a comment to the first part) the Möbius transformation $$ \mu_q(t)=\sqrt q\frac{t+1}{t-1} $$ we still get the squaring rule $$ f(\mu_q(t))=\mu_q(t^2). $$ A difference comes from selecting an appropriate set for the parameter $t$ to range over.

The question specifies that $$ x=\mu_q(t)\qquad(*) $$ should range over $x\in\Bbb{F}_p$. Solving for $t$ from the equation $(*)$ gives $$ t=\frac{x+\sqrt{q}}{x-\sqrt{q}}. $$

Lemma. When $x$ ranges over $\Bbb{F}_p\cup\{\infty\}$ the fraction $t=(x+\sqrt q)/(x-\sqrt q)$ ranges over the multiplicative group of norm one elements of $\Bbb{F}_{p^2}$. In other words, $$ S:=\left\{\frac{x+\sqrt{q}}{x-\sqrt{q}}\bigg\vert\,x\in\Bbb{F}_p\cup\{\infty\}\right\} =\{z\in\Bbb{F}_{p^2}\mid z^{p+1}=1\}. $$ Proof. The non-trivial automorphism of the field $\Bbb{F}_{p^2}$ is clearly $$F:a+b\sqrt q\mapsto a-b\sqrt q.$$ On the other hand, by the well known Galois theory of finite fields, $F$ must be the Frobenius automorphism and we also have $F(z)=z^p$. In particular, $(x\pm\sqrt q)^p=x\mp\sqrt q$ for all $x\in\Bbb{F}_p$. Therefore, if $z=(x+\sqrt q)/(x-\sqrt q)$ we have $$ z^p=F(z)=\frac{x-\sqrt q}{x+\sqrt q}=\frac 1z. $$ This implies that $z^{p+1}=1$. Because the multiplicative group $\Bbb{F}_{p^2}^*$ is cyclic of order $p^2-1=(p-1)(p+1)$, the equation $z^{p+1}=1$ has $p+1$ solutions in $\Bbb{F}_{p^2}$. Different choices of $x$ lead to different values for $z$, so we have found all those solutions. QED.

The rest is then easy. We know that $S$ is a cyclic group of order $p+1$. Repeating the earlier argument we arrive at the following description:

Assume that $q$ is a quadratic non-residue. Write $p+1=2^\ell b$, $b$ odd. Then after $\ell$ iterations the image of $f$ has stabilized. Any further iterations of $f$ will permute this set with the same cycle structure as multiplication by $2$ permutes the residue classes modulo $b$.

As an example consider the case $p=43$, $q=3$ from the top right image in Sangchul Lee's question. Here $p+1=44=2^2\cdot11$. Therefore the graph has two stages of binary branch convergence. Modulo $b=11$ multiplication by two looks like $$(0)(1,2,4,8,5,10,9,7,3,6)$$ explaining the emergence of a 10-cycle (and a fixed point) seen in the image.

Similarly, when $p=113$, we get $p+1=114=2\cdot57$. After a single step of two branches converging we are left to study the cycles of multiplication by two modulo $57=3\cdot19$. Two is a primitive root modulo $19$, so it follows that we get three 18-cycles, a fixed point $0$, and a 2-cycle $(19,38)$. Again, in accordance with the graph in the bottom right.

---

Remark: I cooked up an analogue of the Lemma once to study certain character sums. A colleague used it to study correlation properties of certain families of sequences. See this MathOverflow thread, where Michael Zieve does something similar. Also see Peter Mueller's answer for a generalization. So I am not the inventor. I simply had not seen it before. Anyway, the Lemma is totally analogous to the fact that $$ \left\{\frac{x+i}{x-i}\in\Bbb{C}\bigg\vert\,x\in\Bbb{R}\cup\{\infty\}\right\} $$ is the unit circle of the complex plane.

Answer 2

Whenever $q_1, q_2$ are both quadratic residues modulo $p$, or both quadratic nonresidues modulo $p$, we can find a constant $c \ne 0$ such that $q_2 \equiv c^2 \cdot q_1 \pmod p$. Then multiplication by $c$ induces a graph isomorphism between $G_{p,q_1}$ and $G_{p,q_2}$:

$$ (x,y) \in E(G_{p,q_1}) \iff x^2 - 2xy + q_1 \equiv 0 \\ \iff (cx)^2 - 2(cx)(cy) + c^2q_1 \equiv 0 \iff (cx, cy) \in E(G_{p,q_2}). $$ So in this case, $G_{p,q_1}$ and $G_{p,q_2}$ are going to look the same with only the vertices relabeled (and the relabeling is multiplication by $c$).