6

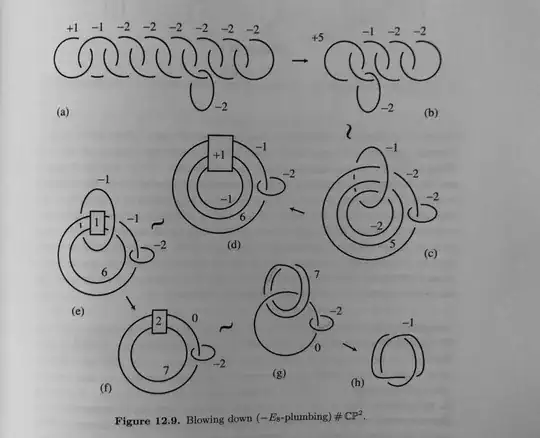
I was trying to show that the 4-manifold described in Kirby diagram as a E8-plumbing (see the diagram below) has the same boundary as the 2-handlebody on the left-handed trefoil with surgery coefficient -1. (which is a standard exercise in geometric topology, and an exercise 5.1.12 in Gompf-Stipsciz) Actually the exercise says that the boundary is the Poincare homology sphere, but it is another matter.

Here is the solution to this question scrapped from Gompf-Stipsicz. Figure (a) is the E8 plumbing, and the relevant Kirby calculus is drawn in order.

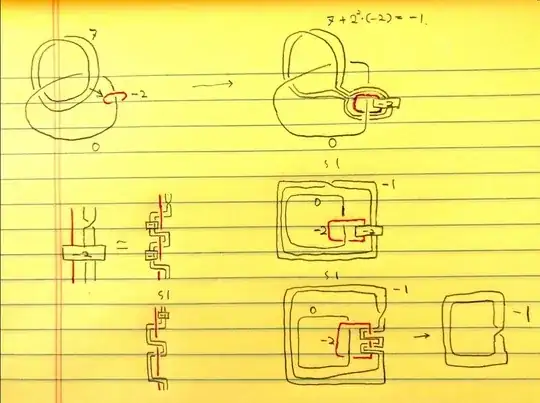
enter image description here

I was able to follow the steps to (g), but wasn't able to make (g) to (h), which is the question on which I'd like to get hint. Below is what I'd tried so far.

enter image description here

I first rotate the meridional unknot(the red unknot) with coefficient -2 a little to make the band sum (along the green arrow) simpler (first figure). Then I made a band sum as shown above, to unlink the knot with slope 7 from the unknot with slope 0 (second figure).

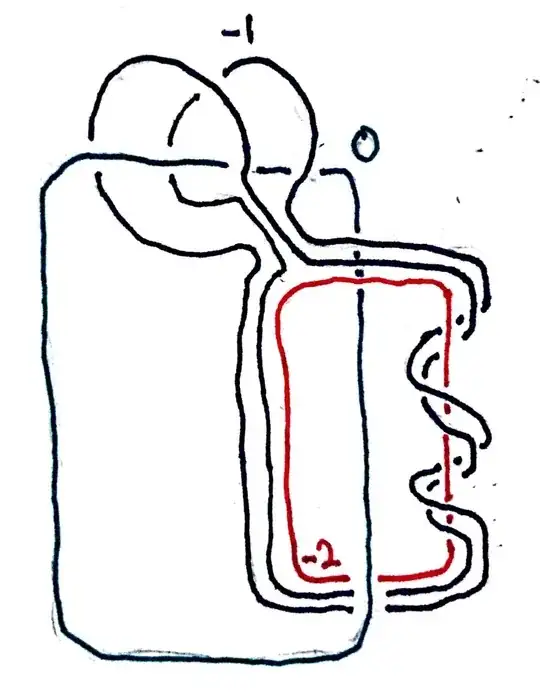
After simplifying the diagram a bit(third figure), we see that the linking between the red unknot and the knot with slope -1 can be made into braid position. A simple argument on the left bottom figures clarify the braiding, so I redrawed the braid part(fourth figure).

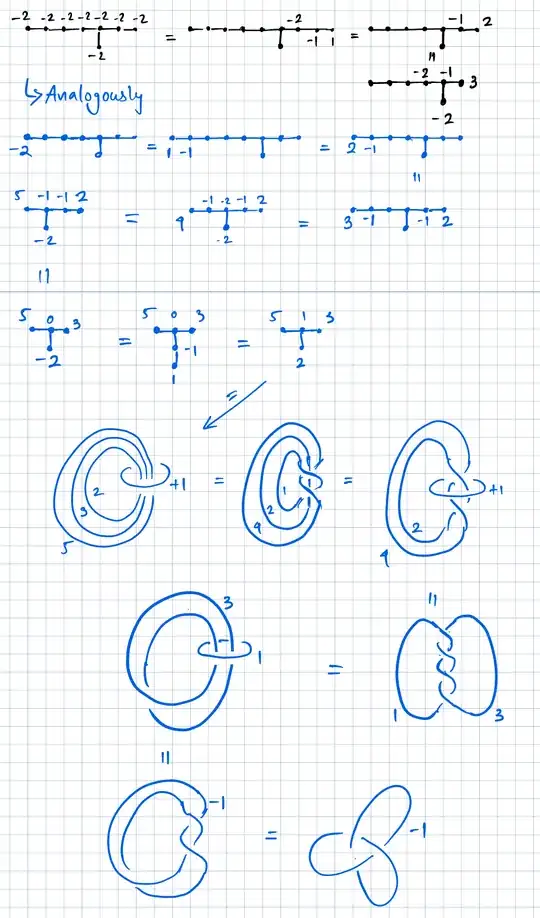
Finally, as the unknot with slope 0 is the meridian of the red unknot, we split a $S^2\times S^2$ (the part consisting of red unknot and its meridian) off from the plane without changing the boundary. The fifth figure is what is left. But this is an unknot!

Okay, now it is clear that I made a mistake at some point, but I couldn't figure out where it is. Can somebody help me point the mistake out, or just elaborate on the step (g) to (h)?

cjackal
  • 2,253
  • On the bottom of the left hand side, a box with a “-1” appeared. That should have been three negative half twists. Either way, this didn’t show up correctly on the bottom right. Those three half twists will give you the trefoil! – Aru Ray Feb 07 '21 at 17:13

2 Answers2

3

This is an old question, but in case anyone finds this helpful, here is a picture:

Kirby diagrams Another way to view the handleslide:

[As @Aru Ray pointed out, the mistake seems to be mixing half-twists and full twists.]

Hrhm
  • 3,555
1

Here is another solution. I have used plumbing fiagrams here for easier manipulation. enter image description here

ryuzaki
  • 38