A curve through two vertices of a triangle, whose tangent lines bisect the area of that triangle

Question

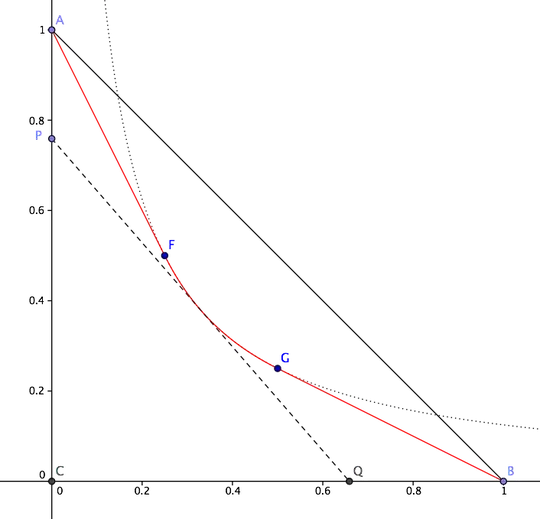
Say we have a triangle $ABC$. I want to find a curve $\gamma:[0,1]\to\mathbb{R}^2$ such that $\gamma(0)=A$, $\gamma(1)=B$ and for all $t\in(0,1)$ the tangent line at $\gamma(t)$ divides $\triangle ABC$ into two pieces of same area (a smaller triangle and a quadrilateral). The curve can be as smooth as you might need of course.

I came up with this problem about a week ago and got a bunch of few equations at first. Now I'm otherwise engaged so I'm posting the problem before I forget about it. Cheers!

Answer 1

To keep things simple, I'll consider a right triangle with unit legs $AC$ and $BC$, with coordinate axes lying along the legs. From this, one can obtain the general case with a suitable coordinate transformation.

If we take $P=(0,t)$ on $AC$, and want to divide the triangle into two equivalent parts through a line cutting $BC$ at $Q$, it is easy to find $\displaystyle Q=\bigg({1\over2t},0\bigg)$, provided $1/2\le t\le 1$. The envelope of all such lines $PQ$ is the hyperbola of equation $xy=1/8$ (dotted in the diagram), but this curve doesn't pass through $A$ and $B$.

We can however take only the central part of this curve, from $F=(1/4,1/2)$ to $G=(1/2,1/4)$ and extend it with two segments $AF$ and $GB$, touching the hyperbola at $F$ and $G$. The resulting composite curve (red in the diagram) is once differentiable and does the requested job.