1

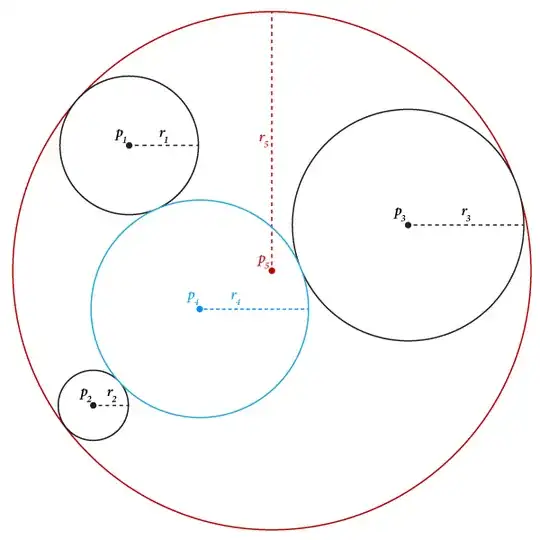
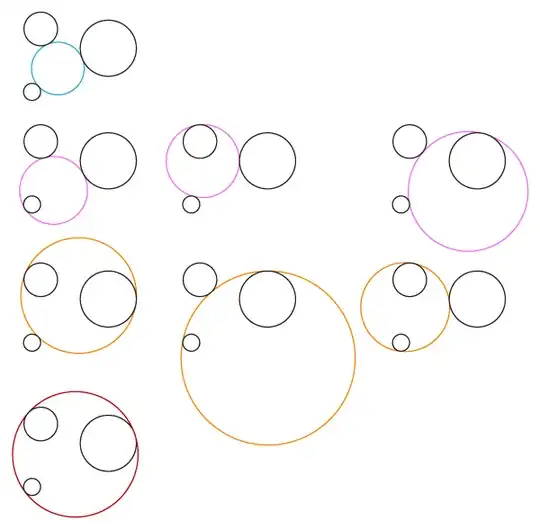Given the positions ($p_1$, $p_2$, $p_3$) and radii ($r_1$, $r_2$, $r_3$) of three circles that are not pairwise tangential, how do you calculate the location and radius of the circle that is pairwise tangential with each of the three original and contains none of them?

The circle that contains all three is a duplicate of this question. This answer to that question shows a geometric way of calculating $p_5$ (and it looks like $p_4$, too), but does not include the formulae needed to calculate the hyperbolae and solve the equations.

Edit: Given three discrete circles, there are 8 circles that can be created which are each pairwise tangent to the discrete circles:

  • 1 that contains none of the circles
  • 3 that contain one circle
  • 3 that contain two circles
  • 1 that contains all three circles

It is the circle that contains none of the original three that I am interested in (shown in blue above and below).

(The original version of this question included the desire to find $p_5$/$r_5$ as well; I'm not actually interested in that circle, as this edit reflects.)

Phrogz
  • 1,880
  • As the answer in the link you provides alludes to, calculating P5 is gonna be a mess. – T. Fo Jan 08 '19 at 18:40
  • @T.Ford Thanks. I'd still like to get it for completeness, but FWIW $p_4$ and $r_4$ are what I really care about. (On the off chance that they are simpler to calculate.) – Phrogz Jan 08 '19 at 18:43
  • Also, in your question when you say the 'smallest (p4, r4)' isnt the circle you are looking for unique? Like more generally I feel as though there should be a result for finding a (unique?) inscribed circle between three non-intersecting circles – T. Fo Jan 08 '19 at 18:47
  • All of the equations for the analytic analogue of that geometric construction are easily found, and, I dare say you already know most of them. Surely you can construct an equation of a circle with given radius and center and that of a line through two points. Solving that system (or some simple vector arithmetic) gets you $G$ and $H$. You might not know off the top of your head how to construct a hyperbola from its foci and a vertex, but you can find that with a search, too. Intersecting the hyperbolas is tedious—it involves solving cubics or quartics—but conceptually simple. – amd Jan 08 '19 at 19:32
  • @T.Ford You are right. I originally thought there were 2 possible pairwise-tangent circles that could be created, and the smaller of the two was the one I want: the one that does not contain any of the circles. As I've edited the question to reflect, there are actually 8 possible circles that can be tangential to the original three; I've also updated the wording to reflect the one I care about. – Phrogz Jan 08 '19 at 21:14
  • @amd I am glad that you believe they are easily found. I spent two hours this morning searching and finding many related topics (like Apollonian circles) but have not found the equations I need. I'd appreciate it if you'd share your knowledge in an answer. – Phrogz Jan 08 '19 at 21:18
  • Finally found that perhaps this question is a duplicate of: https://math.stackexchange.com/questions/1861627/circle-tangent-to-three-circles except perhaps that this question seeks the answer as a formula, while that question seems to be content with a physical solution. – Phrogz Jan 08 '19 at 21:25
  • 2
    Tangent: I'm curious when this problem even has a solution. For example, if we label your three balls $B_1$, $B_2$, and $B_3$, and they all of the same radius and their centers are colinear then there will be no solution as you describe. But to what degree can we shift one of the circles off the line and induce a solution. i.e. for what configurations of the balls is this even solvable? – T. Fo Jan 08 '19 at 21:34
  • Equation of a circle: https://www.purplemath.com/modules/sqrcircle.htm and many others. Equation of a line through two points: http://mathonweb.com/help_ebook/html/lines.htm and many others. For the hyperbolas, use the distance formula and the definition of a hyperbola in terms of distances from its foci. This took all of a few web searches with the obvious search terms to find. – amd Jan 08 '19 at 21:55
  • @T.Ford Not really tangential, I think. Unlike the enclosing circle problem, this one may have no solution for many configurations. Referring back to https://math.stackexchange.com/a/1018382/4241, I wonder if this will be reflected in the number of three-hyperbola intersections. – amd Jan 08 '19 at 22:08
  • What would you like the answer to be when there is no circle externally tangent to all three? – amd Jan 08 '19 at 22:09
  • @amd When there is no answer, then there should be a way of determining that there is no answer. If the equations result in a divide-by-zero in the process of attempting to determine the circle, then that would be one way to detect the failure. – Phrogz Jan 09 '19 at 15:59

0 Answers0