Super hard system of equations

Question

Solve the system of equation for real numbers

\begin{split} (a+b) &(c+d) &= 1 & \qquad (1)\\ (a^2+b^2)&(c^2+d^2) &= 9 & \qquad (2)\\ (a^3+b^3)&(c^3+d^3) &= 7 & \qquad (3)\\ (a^4+b^4)&(c^4+d^4) &=25 & \qquad (4)\\ \end{split}

---

First I used the identity $$(a^2+b^2)(c^2+d^2)=(ac-bd)^2+(bc+ad)^2$$ Use this identity to (4) too and simplify (3), we obtain $$(a^2+b^2-ab)(c^2+d^2-cd)=7$$ And suppose $x=abcd$ use $ac=x /bd , bc=x/ad$ But got stuck...

Answer 1

Hint: $ac=x, bc=y, ad=u, bd=v$, then the equations are

$x+y+u+v=1$

$x^2+y^2+u^2+v^2=9$

$x^3+y^3+u^3+v^3=7$

$x^4+y^4+u^4+v^4=25$

Use Newton-Girard to compute the elementary polynomials. Then you have the polynomial $P(z)= (z-x)(z-y)(z-u)(z-v)$ with variable $z$. Solve the quartic equation $P(z)=0$, and there you have the values $x,y,u,v$ in some order. Note that not in any order: $xv=yu$ must be true, see the definition of these variables.

Of course, once you have $x,y,u,v$, it is easy to compute $a,b,c,d$.

P.S. By this way we can get: $$\{x,y,u,v\}=\{-1,2,\sqrt2,-\sqrt2\},$$ which gives $abcd=-2.$ Up to symmetry, the solution is $(a,b,c,d)= (t, -\sqrt{2}t, -\frac{1}{t}, -\frac{\sqrt{2}}{t})$ for any $t\neq 0$. (By up to symmetry, I mean you can switch $a$ and $b$, you can switch $c$ and $d$, and you can switch the pair $(a,b)$ with $(c,d)$, so there are $8$ symmetries.)

Answer 2

Not really complete, but an interesting result using simple algebraic manipulations.

---

Write: $$\begin{align} a^2+b^2&=(a+b)^2-2ab\\ a^3+b^3&=(a+b)(a^2+b^2-ab)=(a+b)((a+b)^2-3ab)\\ a^4+b^4&=((a^2)^2+(b^2)^2)=\cdots=(a+b)^4+2a^2b^2-4ab(a+b)^2\\ \vdots \end{align}$$ From $(2)$, we have: $$\begin{align} (a^2+b^2)(c^2+d^2)&=((a+b)^2-2ab)((c+d)^2-2cd)=9\\ &=\color{red}{(a+b)^2(c+d)^2}-2ab(c+d)^2-2cd(a+b)^2-4abcd=9 \end{align}$$ But from $(1)$, we know that $(a+b)(c+d)=1$, then the text in $\color{red}{\text{red}}$ is also equal to $1$, so the result above becomes: $$2abcd-ab(c+d)^2-cd(a+b)^2=4\tag{1*}$$ From $(3)$, we have: $$\begin{align} (a^3+b^3)(c^3+d^3)&=\color{red}{(a+b)}((a+b)^2-3ab)\color{red}{(c+d)}((c+d)^2-3cd)=7\\ &=((a+b)^2-3ab)((c+d)^2-3cd)=7\\ &\qquad\vdots\\ &=3abcd-ab(c+d)^2-cd(a+b)^2=2\tag{2*} \end{align}$$ Adding $(1*)$ and $(2*)$, we get $abcd=-2$ and that $\color{pink}{ab(c+d)^2+cd(a+b)^2=-8}$.

---

Now $(4)$ is really tricky, but you can write it as: $$\begin{align} \left((a+b)^4+2a^2b^2-4ab(a+b)^2\right)\left((c+d)^4+2c^2d^2-4cd(c+d)^2\right)&=25 \end{align}$$ Expanding, and we can eliminate $(a+b)^4(c+d)^4$ since it is equal to $1$. Then we have: $$\begin{align} a^2b^2(c+d)^4-2ab(c+d)^2+c^2d^2(a+b)^4+2(abcd)^2-4abc^2d^2(a+b)^2-2cd(a+b)^2-4a^2b^2cd(c+d)^2-4abcd=12 \end{align}$$ Using the fact that $abcd=-2$, then we can shorten the equation above into: $$\color{red}{a^2b^2(c+d)^4+c^2d^2(a+b)^4}+5ab(c+d)^2-10cd(a+b)^2+16=12\tag{3*}$$ However, you can see that the text in $\color{red}{\text{red}}$ looks very close to the square of two sums: $$\color{red}{a^2b^2(c+d)^4+c^2d^2(a+b)^4}=(ab(c+d)^2+cd(a+b)^2)^2-2\color{blue}{abcd(a+b)^2(c+d)^2}$$ However we already know the value of the part in $\color{blue}{\text{blue}}$ to be $-2 \cdot 1$. Now we can write $(3*)$ as: $$(ab(c+d)^2+cd(a+b)^2)^2+6ab(c+d)^2-10cd(a+b)^2=-8$$

---

From here, you can substitute $x=ab(c+d)^2$ and $y=cd(a+b)^2$, which gives two systems of equation: $$(x+y)^2+6x-10y=-8\\ x+y=-8$$ This has one solution: $$x=-\frac{19}2\,\,y=\frac32$$

---

You can try working from here.

Answer 3

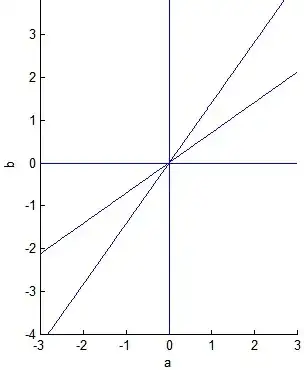
We are going to show that $(a,b)$ belongs to one of the two lines with equations $b=\sqrt{a}$ and $b=\frac{1}{\sqrt{a}}$ as displayed on the following figure. It will give the answer, due to the symmetry of the system of equations with respect to the group of variables $(a,b)$ vs. $(c,d)$. Moreover, we will establish (see (*) at the bottom) that the last equation is superfluous.

Here is the explanation :

Let :

$$S_1:=a+b, \ \ S_2:=c+d, \ \ P_1:=ab, \ \ P_2:=cd$$

The system constituted by the first three equations can be written, with these variables, using classical transformations :

$$\begin{cases} (A) \ &S_1S_2&=&1& \ &\\ (B) \ &(S_1^2-2P_1)(S_2^2-2P_2)&=&9 & \ \implies \ & (C) \ 1-2(P_1S_2^2+P_2S_1^2)+4(P_1P_2)=9\\ (D) \ &(S_1^3-2P_1S_1)(S_2^3-2P_2S_2)&=&7 & \ \implies \ & (E) \ 1-3S_1S_2(P_1S_2^2+P_2S_1^2)+9(P_1P_2)=7. \end{cases}$$

(equations (C) and (E) are obtained by expansion of (B) and (D) resp., using relationship (A)).

Setting

$$\alpha := P_1P_2 \ \text{and} \ \beta := P_1S_2^2+P_2S_1^2,$$

equations (C) and (E) become :

$$\begin{cases} (C) & \ 2\alpha-\beta&=&4\\ (E) & \ 3\alpha-\beta&=&2 \end{cases} \ \ \implies \ \ \alpha=-2 \ \text{and} \ \beta=-8.$$

Using the fact that $S_1S_2=1$ and $\alpha=P_1P_2=-2$, equation $\beta=-8$ becomes :

$$P_1 \frac{1}{S_1^2} - \frac{2}{P_1}S_1^2 = -8$$

i.e.,

$$(F) \ \ \ \ P_1^2 + 8 P_1S_1^2 - 2 S_1^4 =0,$$

which can be considered as a quadratic equation in variable $P_1$ giving two solutions. Due to classical condition

$$(a+b)^2 \geq 2ab \ \iff \ S_1^2 \geq 2P_1,$$

only one of these solutions is eligible :

$$P_1=(-4+3\sqrt{2})S_1^2 \ \ \ \iff \ \ \ ab=(-4+3\sqrt{2})(a+b)^2 \ \ \ \iff \ \ \ (b-\sqrt{2}a)(b-\frac{\sqrt{2}}{2}a)=0$$

whence the result corresponding to the figure.

The parametric equations of the two lines are

$$(a,b)=(p,p \sqrt{2}) \ \ \text{and} \ \ (a,b)=(p,p \frac{\sqrt{2}}{2}), \ \ \text{for any} \ \ p \neq 0$$

Due to the symmetry of equations, we have as well, for any $q \neq 0$ :

$$(c,d)=(q,q \sqrt{2}) \ \ \text{and} \ \ (c,d)=(q,q \frac{\sqrt{2}}{2}).$$

A quick glance at any of the four equations show that necessarily $q=\frac{1}{p}$. We find back in this way all the solutions given by @Claude Leibovici and @A. Pongrácz .

---

(*) In fact, the fourth equation is a consequence of the first three. Here is why :

First of all, relationship (F) is equivalent to :

$$(G) \ \ \ \ S_1^4=\frac12P_1^2+4P_1S_1^2.$$

As the fourth equation can be written :

$$(H) \ \ \ \ (S_1^4+2P_1^2-4P_1S_1^2)(S_2^4+2P_2^2-4P_2S_2^2)=25,$$

using (G) in (H), we get :

$$\frac52P_1^2 \frac52P_2^2=25,$$

which is a tautology due to the fact that $\alpha=P_1P_2=-2.$

Answer 4

This is not an answer but it is too long for a comment.

Looking at this system of equations, I had a very strange feeling (which I cannot explain).

Using a CAS, I solved equations $(1)$, $(2)$, $(3)$ for $a,b,c$ as functions of $d$ and obtained $8$ solutions which are listed below $$\left\{a= \frac{2}{d},b= \frac{\sqrt{2}}{d},c= -\frac{d}{\sqrt{2}}\right\},\left\{a= \frac{\sqrt{2}}{d},b= \frac{2}{d},c= -\frac{d}{\sqrt{2}}\right\},\left\{a= \frac{2}{d},b= -\frac{\sqrt{2}}{d},c= \frac{d}{\sqrt{2}}\right\},\left\{a= -\frac{\sqrt{2}}{d},b= \frac{2}{d},c= \frac{d}{\sqrt{2}}\right\},\left\{a= -\frac{1}{d},b= -\frac{\sqrt{2}}{d},c= -\sqrt{2} d\right\},\left\{a= -\frac{\sqrt{2}}{d},b= -\frac{1}{d},c= -\sqrt{2} d\right\},\left\{a= -\frac{1}{d},b= \frac{\sqrt{2}}{d},c= \sqrt{2} d\right\},\left\{a= \frac{\sqrt{2}}{d},b= -\frac{1}{d},c= \sqrt{2} d\right\}$$

The problem is that, replacing in $(4)$ any of these solutions the resulting equation is $25=25$ !