I have written some python code which was designed to try to solve the following differential equation: $$\ddot{x}+\omega_0^2x=\eta(t),$$ where $\eta(t)$ is the gaussian white noise, with mean 0 and variance 1. The initial conditions are: $$x(0)=\dot{x}(0)=0.$$ The code is given here:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
class HarmonicOdeSolver:
def __init__(self, dt, x0, xd0, omega_squared):
"Inits the solver."
self.dt = dt
self.dt_squared = dt ** 2
self.t = dt
self.omega_squared = omega_squared
self.x0 = x0
self.xd0 = xd0
self.x = [xd0 * dt + x0, x0]
def step(self):
"Steps the solver."
xt, xtm1 = self.x
xtp1 = (2 - self.omega_squared * self.dt_squared) * xt - xtm1 \
+ self.dt_squared * norm.rvs()
self.x = (xtp1, xt)
self.t += self.dt
def step_until(self, tmax, snapshot_dt):
"Steps the solver until a given time, returns snapshots."
ts = [self.t]
vals = [self.x[0]]
niter = max(1, int(snapshot_dt // self.dt))
while self.t < tmax:
for _ in range(niter):
self.step()
vals.append(self.x[0])
ts.append(self.t)
return np.array(ts), np.array(vals)
solver = HarmonicOdeSolver(1e-2, 0, 0, 1)
snapshot_dt = 1.0
ts, vals = solver.step_until(1000, snapshot_dt)
plt.plot(ts, np.sqrt(vals ** 2))
plt.plot(ts, np.sqrt(ts / 2))
The code was taken from and explained here. I naively hoped that I could simply add the following line of code:
self.dt_squared * norm.rvs()
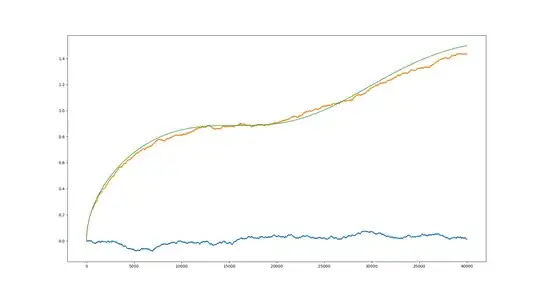
to simulate Gaussian white noise. One problem I have noticed is that the results appear to be highly dependent on the time step used. In a similar post we found that the variance of the oscillator should grow as: $$\sqrt{\langle x(t)^2\rangle}\sim\sqrt{\frac{t}{2}}.$$ I would like to reproduce this result, does anyone know of a simple way to simulate a harmonic oscillator driven by white noise?
EDIT: Thanks for the help WoofDoggy, however, I am still confused. When you turned the ODE into a system of stochasic differential equations should you have not done this: $$dX_t=\dot{X}_tdt,$$ $$d\dot{X}_t=-\omega_0^2X_tdt+dW_t,$$ but instead you have done this: $$dX_t=\dot{X}_tdt+dW_t,$$ $$d\dot{X}_t=-\omega_0^2X_tdt?$$