0

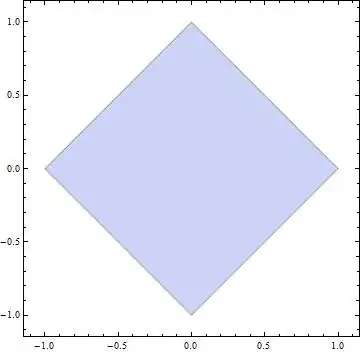
Let $X,Y$ absolutely continuous random variables with density finctions $f_X,f_Y$. Assume that the mutual density $f_{X,Y}$ equals to a constant $c$ in $\{(t,s)\in\mathbb{R}^2:|t|+|s|<1\}$. Are $X,Y$ independent?

I guess I need to use $\int_{-1}^0 \int _{1+s}^{−1−s}f_{X,Y}(x,y)dxdy+\int_0^1\int_{1−s}^{s−1}f_{X,Y}(x,y)dxdy=c$, But I'm not sure how can it help me.

The defenition of independent random variables is random variables $X,Y$ such that $\forall(t,s)\in \mathbb{R}^2, F_{X,Y}(t,s)=F_X(t)F_Y(s)$.

StubbornAtom
  • 17,932
J. Doe
  • 1,404
  • 9
  • 25
  • Your thoughts/work? – StubbornAtom Dec 26 '18 at 17:40
  • I guess I need to use $\int_{-1}^0 \int {-1-s}^{1+s} f{X,Y}(x,y)dxdy+\int_0^1 \int {s-1}^{1-s} f{X,Y}(x,y)dxdy=c$ (suppose that $f_{X,Y}(a,b)=c$ for all $(a,b)$ in the above set). But I'm not sure how can it help me.@StubbornAtom – J. Doe Dec 26 '18 at 17:47
  • Where have you checked independence? What definition of independence have you tried working with? Please add your attempts in your post, not in comments. – StubbornAtom Dec 26 '18 at 17:58
  • @StubbornAtom Done – J. Doe Dec 26 '18 at 18:04
  • 1
    By sketching a picture of the region $S={(x,y):|x|+|y|<1}$ you will see that Support$(X_1)\times$ Support$(X_2)\ne S$, violating a necessary condition of independence of $X_1$ and $X_2$. – StubbornAtom Dec 26 '18 at 18:28
  • 1
    Just to complement @StubbornAtom: also see https://math.stackexchange.com/questions/663175/independence-in-rectangular-region – Just_to_Answer Dec 26 '18 at 18:34
  • 1
    and one more note: from the picture of the support (the diamond centered at the origin), think about the locations inside the unit square outside the diamond. For those the marginals will be non-zero, but the joint will be zero. – Just_to_Answer Dec 26 '18 at 18:36
  • 1
    An illustration of @StubbornAtom's comment can be found my answer where I called it the eyeball test. If the support of the joint pdf is not a rectangle with sides parallel to the axes, then the random variables are dependent: no need for finding the marginal densities and checking whether or not $f_{X,Y}(x,y)$ equals the product of $f_X(x)$ and $f_Y(y)$ everywhere in the plane. – Dilip Sarwate Dec 26 '18 at 23:17

1 Answers1

1

The joint support of $(X,Y)$ is the set

$$S=\left\{(x,y)\in\mathbb R^2:|x|+|y|\le 1\right\}$$

Sketch the region $S$. It should look like this picture:

enter image description here

Let $S_1$ and $S_2$ be the supports of $X$ and $Y$ respectively. Clearly,

$$S_1=\{x\in\mathbb R:-1\le x\le 1\}=\{y\in\mathbb R:-1\le y\le 1\}=S_2$$

A necessary condition of independence of two jointly distributed random variables is that their joint support must be the Cartesian product of their marginal supports.

That is, $X$ and $Y$ are independent only if $\text{supp}(X,Y)=\text{supp}(X)\times \text{supp}(Y)$.

[Simplest example: Consider $(X,Y)$ uniform on the unit square.]

Here of course $S\ne S_1\times S_2$, as should be evident from the picture above. Hence $X$ are $Y$ are dependent.

Equivalently, observe that $$P\{0.5\le X\le 1,0.5\le Y\le 1\}=0\ne P\{0.5\le X\le 1\}P\{0.5\le Y\le 1\}$$

So no need really to check whether $F_{X,Y}=F_{X}F_Y$ or $f_{X,Y}=f_Xf_Y$ for independence of $X$ and $Y$.

Also see this relevant answer from Dilip Sarwate.

StubbornAtom
  • 17,932
  • I only know that $f_{X,Y}$ is constant in the diamond, but it could be equal to $c=0$. Doesn't it contradict the support of $f_{X,Y}$? @StubbornAtom – J. Doe Dec 27 '18 at 12:22
  • @J.Doe How could $f_{X,Y}$ equal zero ? The region $S$ has a finite area, $f_{X,Y}$ equals the reciprocal of that area whenever $|x|+|y|<1$. – StubbornAtom Dec 27 '18 at 12:34
  • @J.Doe "contradict the support of $f_{X,Y}$" ?? – StubbornAtom Dec 27 '18 at 12:40