1

If
$x_1+x_2+x_3 = c_1$
$x_2+x_3+x_4 = c_2$
$x_3+x_4+x_5 = c_3$
.
.
$x_{99}+x_{100}+x_1 = c_{99}$
$x_{100}+x_1+x_2 = c_{100}$

$x_i$ denote variables and $c_i$ denote constants.
How to calculate $x_1,x_2,\dots,x_{100}?$

Jyrki Lahtonen
  • 140,891
Navneet Hingankar
  • 27
  • The variables here are reals? That can be positive and negative? – alan2here Dec 14 '18 at 15:50
  • 1
    yes they are real. – Navneet Hingankar Dec 14 '18 at 15:52
  • If this were drawn visually, it'd seem like some puzzles in the back of newspapers. You can always do the thing with vectors/matrices to solve this sort of system of equations. But I'd expect there to be neater solution for a specific case like this. Also you could have it go 1 to N rather than 1 to 100. – alan2here Dec 14 '18 at 16:13
  • how can i find just any one element i will use it for finding other elements – Navneet Hingankar Dec 14 '18 at 16:32
  • 1
    @alan2here For general $N$ there will be surprises. Should $N$ be divisible by three, the matrix of the system is singular. This can, sort of, be seen from the circulant view Damien suggested. – Jyrki Lahtonen Dec 14 '18 at 20:32
  • Anyway, the matrix of this system is circulant. Essentially you need to do a discrete Fourier transform, and then divide the components by the eigenvalues, "to equalize" as Damien colorfully put it. See here for this way of analyzing a very similar matrix. – Jyrki Lahtonen Dec 15 '18 at 04:33

2 Answers2

2

Edit: this answer was largerly edited, but keeping the same methodology, dealing with this problem by pure polynomial manipulation

Let us call $D$ the cyclic delay operator, the matrix is equal to $A=I+D+D^2$ with $D^{100}=I$

All circulant matrices can be represented in this way. A key point here is that the subset (ring) of circulant matrices is commutative, which allows classical algebric manipulations, here formal polynomial manipulation.

We first note that

$$\sum_{i=0}^{99} D^i = (I+D+D^2) \sum_{i=0}^{32}D^{3i} + D^{99}$$ $$ D^{99} = D^{-1}$$ $$(I+D+D^2) \sum_{i=0}^{99} D^i = 3\, \sum_{i=0}^{99} D^i $$

It follows: $$(I+D+D^2)^{-1} = \frac{1}{3} \sum_{i=0}^{99} D^i - \sum_{i=0}^{32} D^{3i+1}$$

And finally: $$x_j = \frac{1}{3} \sum_{i=1}^{100} c_i - \sum_{i=0}^{32} c_{j+3i+1} $$

When the indices $j+3i+1$ must be understood in a 'cyclic' way.

Note 1: the matrix $A$ corresponds to a cyclic filtering operation. The inversion can be interpreted as equalization

Note 2: all circulant matrices have same eigenvectors, corresponding to the DFT matrix. This can be used for example to show that the corresponding ring is commutative. It could be used also to perform the matrix inversion ("equalization in the frequency domain"). This proves that when an inverse of a circulant matrix exists, this matrix is circulant

amWhy
  • 210,739
Damien
  • 1,772
  • How could i use to solve this set of equations,would u please explain – Navneet Hingankar Dec 14 '18 at 17:06
  • Yes (the upvote is mine), this will work. As long as you remember that the condition $D^{100}=1$ makes your time axis cyclic, meaning that you need to do a DFT. Division by eigenvalues works fine because the zeros of $A$ are the third roots of unity, and we are plugging in 100th roots of unity. $\gcd(3,100)=1\implies$ no problems. – Jyrki Lahtonen Dec 15 '18 at 05:11
  • @JyrkiLahtonen Thank you.I need to complete this answer. I know about DFT use for circulant matrices. My first intention is to use a polynomial approach, using the fact that the relevant subset (ring) is commutative, allowing classical algebric manipulations. If it appears to be too fastidious, I will come back to DFT (frequency domain equalization !) – Damien Dec 15 '18 at 08:54
  • @NavneetHingankar Is it clear enough now ? – Damien Dec 15 '18 at 15:50
0

I inverted the matrix of coefficients for the $10 \times 10$ case in a spreadsheet. If we call the entries of the matrix $a_{ij}$ we get $$a_{ij}=\begin {cases} -\frac 23&j \gt i, j-i \equiv 1 \pmod 3 \\ -\frac 23 & i \gt j,i=j \equiv 0 \pmod 3 \\\frac 13 & \text {otherwise} \end {cases}$$ You can multiply the column matrix of the $c_i$ by this to get the $x_i$. I am sure the pattern will continue for all matrices of size $1 \bmod 3$. You can verify the inverse by multiplying it by your coefficient matrix. It will take some keeping track of indices, but it should work. An image of three times the inverse in the $10 \times 10$ case is below. 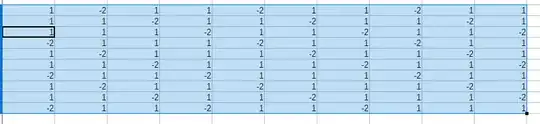enter image description here

This gives $$x_1=\frac 13 \sum_{i=1}^{100} c_i-\sum_{j=1}^{33}c_{3j-1}$$ and all the others are cyclic shifts of this.

Ross Millikan
  • 383,099