2

How can we find minimum radius of circle which contains $\arctan^2(x)+\arctan^2(y)=a$, where I think $a<\pi/2$?

For example I have some plots from WolframAlpha and I see it depends on $a$.

But have no idea how to find maximum radius because this is not simple implicit function.

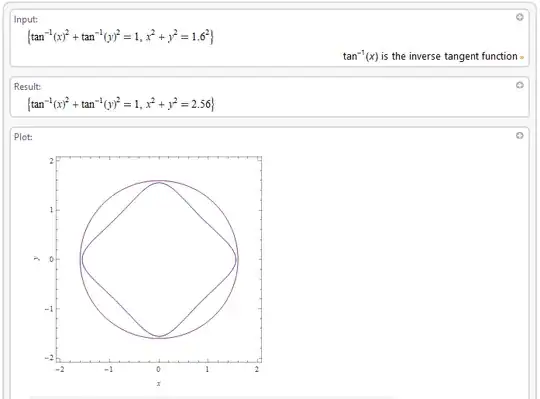
enter image description here

Tag
  • 139
  • 6
  • This might be amenable to using polar coordinates. – hardmath Dec 07 '18 at 16:23
  • @hardmath I believe it becomes an atrocious mess. Lagrange multipliers might be better? – Federico Dec 07 '18 at 16:29
  • If we take derivative with respect to $x$ we and set $y'=0$ we will find that $x=0$. Isn't that correct proof? – Tag Dec 07 '18 at 16:34
  • @Federico yes, but perhaps we can do it neatly with a change of variables. – hardmath Dec 07 '18 at 16:35
  • @user8053696: no, the maximum radius might come at $x=y$. In that case the derivative would be $\pm 1$ – Ross Millikan Dec 07 '18 at 16:39
  • Just looking at plots for various values of $a$ convinces me that the maximum radius comes along the axes, like on the plot you show. Then you get $r=\tan \sqrt a$ easily. I don't have a proof that this is true. – Ross Millikan Dec 07 '18 at 16:41
  • @RossMillikan that's precisely what i'm saying in my answer – Federico Dec 07 '18 at 16:42
  • That's a cute way of getting a quasisquare with rounded corners! I'll have a look at parametrisations of that for arbitrarily choosing the sharpth of the corners ... I find that kind of thing extremely interesting, & sent in a post on it a while back. – AmbretteOrrisey Dec 07 '18 at 18:55

1 Answers1

2

Seems like the smallest circle is always tangent at $x=0$ or $y=0$. So you can put $\arctan(x)^2=a$ and solve $x=\tan\sqrt a$. This would be the radius.

Edit: let's make it rigorous.

Let's maximize $x^2+y^2$ with the constraint $\arctan(x)^2+\arctan(y)^2=a$. By symmetry we can work in the positive quadrant. With Lagrange multipliers we find $$ \left(\frac{\arctan(x)}{1+x^2},\frac{\arctan(y)}{1+y^2}\right) = \lambda (x,y), $$ therefore (unless $x=0$ or $y=0$, which are easily seen to be stationary points) we have $$ \frac{\arctan(x)}{(1+x^2)x} = \frac{\arctan(y)}{(1+y^2)y}. $$ We want to show that the only possibility is $x=y$. The we need an argument to say that this is a minimum and not a maximum.

As a matter of fact, the function $\frac{\arctan(x)}{(1+x^2)x}$ is decreasing, so this shows that $x=y$ are the only solutions. Its derivative is in fact $$ \begin{split} \frac{d}{dx}\frac{\arctan(x)}{(1+x^2)x} &= \frac{2}{x \left(x^2+1\right)^2}-\frac{2 \arctan(x)}{x^2 \left(x^2+1\right)}-\frac{4 \arctan(x)}{\left(x^2+1\right)^2} \\ &< \frac{2}{x \left(x^2+1\right)^2}-\frac{2 \arctan(x)}{x^2 \left(x^2+1\right)} \\ &= -2 \frac{(1+x^2)\arctan(x)-x}{(x+x^3)^2} < 0. \end{split} $$

You may rightfully wonder why is $(1+x^2)\arctan(x)-x>0$? Well, it vanishes at $0$ and its derivative is $2x\arctan(x)>0$.

So, why is $x=y$ a minimum? Well, we just need to compare it with the point at $y=0$.

The values of $x^2+y^2$ at the two points are respectively $2(\tan\sqrt{a/2})^2$ and $(\tan\sqrt a)^2$. Since the function $f(t)=(\tan\sqrt t)^2$ is convex and vanishes at $0$, it is superadditive, implying that $2f(a/2)\leq f(a)$.

Bonus

I'd like to add one little piece, related to proving that $(1+x^2)\arctan(x)-x$ is increasing. The insight is that it is of the form $\frac{g(x)}{g'(x)}-x$ with $g$ concave. Then it's derivative is $-\frac{g(x)g''(x)}{g'(x)^2} \geq 0$. I don't know if this general detail might be useful to someone.

Federico
  • 6,010