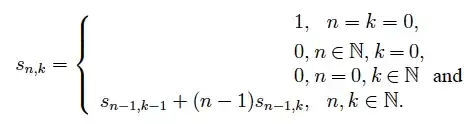3

In our Combinatorics Script it is written, that $$s_{n+1,k+1} = \sum_{i = 0}^{n} \binom{i}{k}s_{n,i}$$ for $n,k \in \mathbb{N}$.

The problem is that I can't find a combinatorial proof for that, not in the Script and not online.

I thought about looking at a set $S_{n,k}$ of the permutations of $[n]$, which are the products of exactly $k$ disjoint cycles, but that's just a thought...

The Stirling numbers of the first kind are defined recursively by:

enter image description here

And how can one give a bijection between a set of the cardinality $\sum_{i=0}^{n} \binom{i}{k} s_{n,i}$ and $S_{n+1, k+1}$?

Apparently defining such a transformation can be extracted from the following example. Does someone know how it's done?

$(1,3,8,7)(2,9,5)(4,12,10,6)(11,13) \to (14,4,12,10,6,1,3,8,7)(2,9,5)(11,13)$

NotEinstein
  • 307
  • What is definition of $S(a,b)$? And of $s-{u,v}$ [lower case $s$ with subscripts] Or should the latter be also upper case as in title? – coffeemath Dec 06 '18 at 07:16
  • 1
    Are you sure these are second kind Stirling numbers? Your example contains permutations, not partitions. – Angina Seng Dec 06 '18 at 07:30
  • @LordSharktheUnknown Sorry, you are right. It was the first kind. I edited it. – NotEinstein Dec 06 '18 at 07:38
  • Can you please give a reference to your script? Are you sure you have written all the correct correctly? Also, you're "thought" in the third line, isn't it the definition of Stirling numbers of the first kind (should've been lowercase s)? – sonu Dec 06 '18 at 09:38

2 Answers2

4

You know what method works (almost) always to prove an identity about a sequence defined inductively? Induction.

Base case is trivial.

$$ s_{n+1,k+1}=s_{n,k}+ns_{n,k+1}= \sum_{i = 0}^{n-1} \binom{i}{k-1}s_{n-1,i}+ n\sum_{i = 0}^{n-1} \binom{i}{k}s_{n-1,i}$$$$= \sum_{i = 0}^{n-1} (\binom{i}{k-1}s_{n-1,i}+ \binom{i}{k}s_{n-1,i}) +(n-1)\sum_{i = 0}^{n-1} \binom{i}{k}s_{n-1,i}$$$$=\sum_{i = 0}^{n-1} \binom{i+1}{k}s_{n-1,i} +(n-1)\sum_{i = 0}^{n-1} \binom{i}{k}s_{n-1,i}$$$$=\sum_{i = 1}^{n} \binom{i}{k}s_{n-1,i-1} +(n-1)\sum_{i = 0}^{n-1} \binom{i}{k}s_{n-1,i}$$$$=\sum_{i = 0}^{n-1} \binom{i}{k}s_{n,i}+\binom{n}{k}=\sum_{i = 0}^{n} \binom{i}{k}s_{n,i}$$ $\blacksquare$

Anubhab
  • 2,078
3

Let $A=\{a_1,\cdots,a_m \} $ be a finite set, that does not contain the element $n+1$. We begin by noting a one to one correspondence between permutations of this set and the conjugacy class of $A \cup \{n+1 \}$. Given an element $\pi \in S_A$ ($\pi(a_i)=\pi_{a_i}$) we form an element of $S_{A \cup \{n+1 \}}$ by \begin{eqnarray*} \pi \rightarrow (n+1,\pi_{a_1}, \cdots , \pi_{a_m} ). \end{eqnarray*} We shall now use this to establish the following formula \begin{eqnarray*} \sum_{i=k}^{n} {n \brack i} \binom{i}{k} = {n+1 \brack k+1}. \end{eqnarray*} Let $ \sigma$ be an element of $S_n$ with $i$ cycles. Choose $k$ of these cycles and let $A$ be the set of elements in the other $i-k$ cycles. Now form an element of $S_{n+1}$ consisting of the $k$ chosen cycles and a cycle formed by the correspondence $S_A \rightarrow S_{A \cup \{n+1 \}}$ defined above. Now let $k$ vary over its admissable values and the formula is proven.

Donald Splutterwit
  • 37,323