What's wrong with this Penrose pattern?

Question

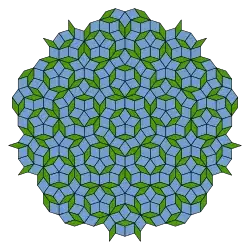
I programmed the Penrose tiling by projecting a portion of 5D lattice to 2D space, by the "cut and project" method described in

1. Quasicrystals: projections of 5-D lattice into 2 and 3 dimensions, H. Au-Yang and J. Perk.
2. Generalised 2D Penrose tilings, A. Pavlovitch and M. Kléman

The orthonormal basis is chosen as $$ M=\sqrt{\frac{2}{5}} \begin{bmatrix} \cos 0 & \cos \frac{2\pi}{5} & \cos \frac{4\pi}{5}& \cos \frac{6\pi}{5}& \cos \frac{8\pi}{5} \\ \sin 0 & \sin \frac{2\pi}{5} & \sin \frac{4\pi}{5}& \sin \frac{6\pi}{5}& \sin \frac{8\pi}{5} \\ \cos 0 & \cos \frac{4\pi}{5} & \cos \frac{8\pi}{5}& \cos \frac{12\pi}{5}& \cos \frac{16\pi}{5} \\ \sin 0 & \sin \frac{4\pi}{5} & \sin \frac{8\pi}{5}& \sin \frac{12\pi}{5}& \sin \frac{16\pi}{5} \\ \frac{1}{\sqrt {2}} & \frac{1}{\sqrt {2}} & \frac{1}{\sqrt {2}} & \frac{1}{\sqrt {2}} & \frac{1}{\sqrt {2}}\\ \end{bmatrix} $$ Each row presents a basis vector, i.e. $$ M_i\cdot M_j=0, \;\;\textrm{for } i<j.$$ and $$||M_i||=1, \;\;\textrm{for } 1\leq i \leq 5. $$

$M$ consists of the parallel operator (representing the physical space) $$ A=\begin{bmatrix} M_1\\ M_2 \\ \end{bmatrix}= \begin{bmatrix} \cos 0 & \cos \frac{2\pi}{5} & \cos \frac{4\pi}{5}& \cos \frac{6\pi}{5}& \cos \frac{8\pi}{5} \\ \sin 0 & \sin \frac{2\pi}{5} & \sin \frac{4\pi}{5}& \sin \frac{6\pi}{5}& \sin \frac{8\pi}{5} \\ \end{bmatrix} $$ and the perpendicular operator $$ B=\begin{bmatrix} M_3\\ M_4 \\ M_5 \\ \end{bmatrix}=\begin{bmatrix} \cos 0 & \cos \frac{4\pi}{5} & \cos \frac{8\pi}{5}& \cos \frac{12\pi}{5}& \cos \frac{16\pi}{5} \\ \sin 0 & \sin \frac{4\pi}{5} & \sin \frac{8\pi}{5}& \sin \frac{12\pi}{5}& \sin \frac{16\pi}{5} \\ \frac{1}{\sqrt {2}} & \frac{1}{\sqrt {2}} & \frac{1}{\sqrt {2}} & \frac{1}{\sqrt {2}} & \frac{1}{\sqrt {2}}\\ \end{bmatrix} $$

The 5D lattice points are integer combinations of basis such as $$ p=i \begin{bmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ \end{bmatrix} + j\begin{bmatrix} 0\\ 1\\ 0\\ 0\\ 0\\ \end{bmatrix} +\dots, \;\; i,j,\dots \in \mathbb{Z} $$

A 5D cube (centered at origin) is projected into 3D as polytope $$ v'= B v, \;\; v\in hypercube $$ so that I can check whether a $p$ is inside this polytope (20 faces). This is called "cutting" the 5D lattice points.

The resultant 2d projection $Ap$ is

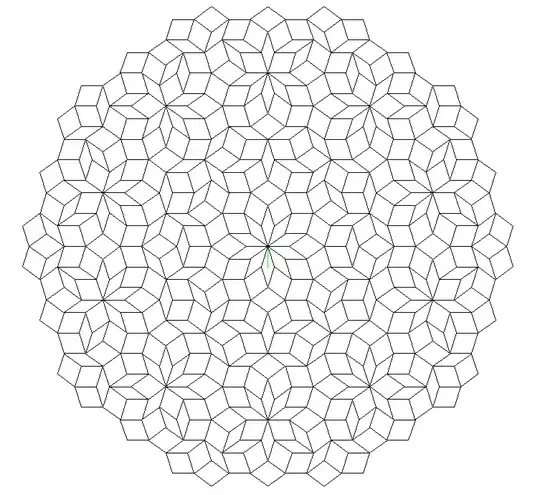
Everything works fine, however, my result differs from the "standard" one (e.g. in wiki page) as follows

Is this a mistake or an alternative view of the same tiling?

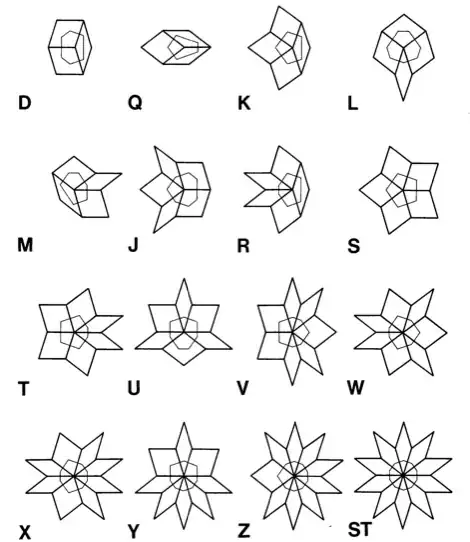
Finally, I find this image (from Vertex Frequencies in Generalized Penrose Patterns, by E. Zobetz and A. Preisinger)

where the center of standard tiling exhibits the "S" pattern, while the center of my version has the "ST" pattern. But what does it mean exactly?

Answer 1

The Wikipedia article states "Therefore, a finite patch cannot differentiate between the uncountably many Penrose tilings, nor even determine which position within the tiling is being shown". Thus they could be the same tiling but differently centered.

In particular, aside from the two dimensional shifting of Penrose tilings, if a higher dimensional lattice is shifted before projecting to two dimensions, then a similar situation holds.

Answer 2

I believe your constant $\gamma$ to be essentially the same as the constant $y$ in de Bruijn 1981 cited below. I don't use your exact projection matrices though like you I do use matrices involving sines and cosines of multiples of $2\pi/5$. I ran into similar issues, and for me, setting $y_i=\epsilon$ for $\epsilon>0$ as small as I could represent it got rid of the forbidden intersections like the ST intersection. Somewhere, distantly, in my tiling is an ST intersection but I regard that as approximation error and simply work to keep it distant.

So I recommend $\gamma_i=\epsilon$. It may not work because your matrices are in a different basis from mine, but I bet some straightforward combination of $\pm\epsilon$ will do the trick for you.

Additionally if it would be helpful I can dig through my notes to get my derivation.

de Bruijn, N. G. "Algebraic theory of Penrose's non-periodic tilings of the plane. I, II: dedicated to G. Pólya." Indagationes Mathematicae 43.1 (1981): 39-66.

Answer 3

I wrote to Prof. J.H.H.Perk, this is a quote from his email:

You want to make a different choice (the translation on lattice $p$), so that no three grid lines (3) pass through the same point. This requires that at least three of the five gammas are nonzero. Generically then you get a regular Penrose tiling, but you can still get singular Penrose tilings like the one for all gammas zero. Those choices are everywhere dense, like rationals are dense within the reals, but only infinitesimal part of them.

Which means the 5D lattice points are $$ p=\gamma_1 \begin{bmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ \end{bmatrix} + \gamma_2 \begin{bmatrix} 0\\ 1\\ 0\\ 0\\ 0\\ \end{bmatrix} + \gamma_3 \begin{bmatrix} 0\\ 0\\ 1\\ 0\\ 0\\ \end{bmatrix} + \gamma_4 \begin{bmatrix} 0\\ 0\\ 0\\ 1\\ 0\\ \end{bmatrix} + \gamma_5 \begin{bmatrix} 0\\ 0\\ 0\\ 0\\ 1\\ \end{bmatrix} $$ However, I have not figured out the correct $\gamma_1,\dots,\gamma_5 \in \mathbb{R}$.

If $\gamma_i=0$ (the lattice is not shifted), the 3D window is as follows,

which contains ten points. This is against the case of Penrose pattern whose window should contain five points.