I've been asked to find the curl of a vector field in spherical coordinates. The question states that I need to show that this is an irrotational field.
I'll start by saying I'm extremely dyslexic so this is beyond difficult for me as I cannot accurately keep track of symbols.
$\mathbf{F}(r,\theta,\phi )=r^2 \sin^2\theta (3\sin\theta \cos\phi \mathbf{e}_{r}+3\cos\theta \cos\phi \mathbf{e}_{\theta }-\sin\phi \mathbf{e}_{\phi })$
None of the examples in the text look remotely like this so I'm completely lost. I can only assume that I'm supposed to multiply out the first term across the brackets, but no similar examples are provided and I can't seem to find any online so I can't tell if this is what to do or not.
I started out by finding my formula using the matrix method in my handbook, that went ok.
I then wrote out my equation using the determinants and simplified my terms symbolically which also went ok.
$\mathbf{e}_{r}\left ( \frac{1}{r} \frac{\partial F_{\phi }}{\partial \theta }-\frac{1}{r\sin\theta }\frac{\partial F_{\theta }}{\partial \phi } \right )+e_{\theta }\left ( \frac{1}{r\sin\theta }\frac{\partial F_{r}}{\partial \theta }-\frac{\partial F_{\theta }}{\partial r} \right )+e_{\phi }\left (\frac{\partial F_{\theta }}{\partial r} -\frac{1}{r}\frac{\partial F_{r}}{\partial \theta }\right )$
I then tried to start by multiplying the bracket out and finding my partial derivatives. Then I placed my terms in the formula.
In all example cases, there are instances where zeros appear as the partial derivatives and cancellation of terms is obvious.
When I put these partials into my formula, nothing seems to cancel with anything.
I don't know if I have something conceptually wrong or if I have something dyslexically wrong.
I'm out of ideas and I've literally taken 6 hours to get this far with it, and 30 minutes just to type this question. I need help!
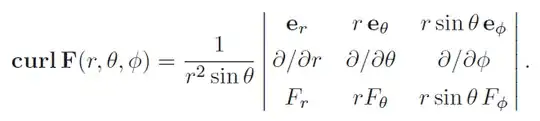

Once I realised I needed to multiply the matrix coefficients before starting the process, it all clicked.
– C. Wolfe Nov 25 '18 at 22:53