Expected profit of my simple board game

Question

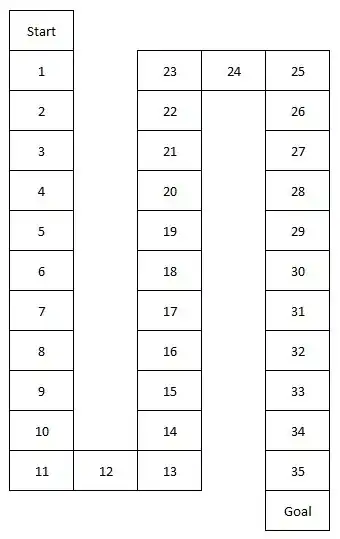
How to play:

Use 1 host and at least 1 player

Each player has to toss fair six-sided dice to go to goal.

If the player is at the 35th cell and tosses 2 or more, he can go to goal aa same as he tosses 1.

If the player reaches the goal in 9 tossing or less, the host has to pay to that player 1$ per 1 tossing less than 10.

For example, if the player reaches the goal in 7 tossing, host have to pay 3$ to that player.

If the player reaches the goal in 11 tossing or more, that player has to pay to host 1$ per 1 tossing more than 10.

For example, if the player reaches the goal in 12 tossing, that player has to pay 2$ to host.

If the player reaches the goal in 10 tossing, no one has to pay.

Each game will end only if the player reaches the goal.

Player can't pay 1$ and start new game if he can't reaches the goal in 11th tossing.

What is expected profit of host per player for each game?

As much as I know for this game, The expected value in rolling a six-sided die is 3.5. The expected value of distance in 10 tossing is 35-cell but the goal is at 36-cell distance so expected profit of host is positive. If the goal is at 35th-cell, expected profit of host is 0. But I have no idea to calculate.

Answer 1

Here is the exact computation, taking all possible games into account. Idea: Consider the polynomial $$p_j(x):=(x+x^2+x^3+x^4+x^5+x^6)^j\ .$$ The coefficient $[x^k]p_j(x)$ gives the number of $j$-tosses histories that bring the player exactly to square $k$. Since I'm not interested in squares $k\geq36$ I truncate $p_j(x)$ after the $x^{35}$ term. In this way I obtain the "truncated series" ${\tt s[j]}$. The sum $\sum_{k=0}^{35} [x^k]p_j(x)$ counts the number of games that are not over after $j$ tosses. Dividing this sum by $6^j$ gives the probability $p(j)$ that the game is not yet over after $j$ tosses, and $q(j):=p(j-1)-p(j)$ is the probability that the game ends with the $j^{\rm th}$ toss. The expected gain for the host then is $\sum_{j=1}^{36} (j-10)q(j)$.

If the goal is at square $35$ instead of $36$ the corresponding value is $0.476195$, and for $34$ it is $0.190481$ in favor of the host. In any case I suggest you write your own program and tune the parameters as desired.