Let $ABCD$ be a fixed convex quadrilateral and $P$ be an arbitrary point. Let $S,T,U,V,K,L$ be the projections of $P$ on $AB,CD,AD,BC,AC,BD$ respectively. Let $X,Y,Z$ be the midpoints of $ST,UV,KL$. Is it true that the angles of triangle $\triangle XYZ$ do not depend on the position of $P$?
I drew a figure on my computer and it seems that the angles of triangle $\triangle XYZ$ do not change with the position of point P:
(my original research)
Here is the proof using Mathematica and simple analytical geometry. In theory, you can do all this by hand, there is nothing special in it. But in real life, you need a computer.
Math involved in the proof is elementary and I did not have to use trigonometry until the very last step.
WLOG, we can assume that $A(0,0)$, $B(0, 1)$, $C(x_C,y_C)$, $D(x_D,y_D)$, $P(x_P,y_P)$:
a = {0, 0}; b = {0, 1}; c = {xc, yc}; d = {xd, yd}; p = {xp, yp};
We need just two functions. The first one calculates dot product of two vectors:
dotProduct[a_, b_] := Sum[a[[i]] b[[i]], {i, 1, Length[a]}];
The second one is used to find the coordinates of projection of point P to line AB:
projection[a_, b_, p_] := Module[
{c, xc, yc, s, k},
c = {xc, yc};
s = Solve[{c - a == k (b - a),
dotProduct[b - a, c - p] == 0}, {xc, yc, k}];
Return[c /. s[[1]]];
];
That's all that we need. The rest is simple and completely straightforward. We are going to "read" the picture and calculate coordinates of all the points.
First, let's calculate coordinates of points $S,T,U,V,K,L:$
s = projection[a, b, p];
t = projection[c, d, p];
u = projection[a, d, p];
v = projection[b, c, p];
k = projection[a, c, p];
l = projection[b, d, p];
Coordinates of points $X,Y,Z$ are:
x = (s + t)/2;
y = (u + v)/2;
z = (k + l)/2;
We need two vectors: $\vec{XY},\vec{XZ}$:
xy = y - x;
xz = z - x;
And, finally, we are ready to calculate the angle $YXZ$ from the formula:
$\cos^2\angle YXZ=\frac{(\vec{XY} \cdot \vec{XZ})^2}{(\vec{XY} \cdot \vec{XY})(\vec{XZ} \cdot \vec{XZ})}$
...or in Mathematica:
cosXsquared = Together[dotProduct[xy, xz]^2/(dotProd[xy, xy] dotProduct[xz, xz])]
And the final result is:
$$\cos^2\angle YXZ=\\\frac{\left({x_C}^2 {x_D}^2+{x_C}^2 {y_D}^2-{x_C}^2 {y_D}+{x_C} {x_D}+{x_D}^2 {y_C}^2-{x_D}^2 {y_C}+{y_C}^2 {y_D}^2-{y_C}^2 {y_D}-{y_C} {y_D}^2+{y_C} {y_D}\right)^2}{\left({x_C}^2+{y_C}^2\right) \left({x_C}^2+{y_C}^2-2 {y_C}+1\right) \left({x_D}^2+{y_D}^2\right) \left({x_D}^2+{y_D}^2-2 {y_D}+1\right)}$$
Depsite the fact that $x_P,y_P$ can be easily observed in all intermediate results, the coordinates of point $P$ have magically disappeared from the final one.
In the same way you can prove that the other two angles of triangle $\triangle XYZ$ are independent from the location of point $P$.
Hint: One way to solution is with a use of a following lemma:
Lemma: Let the points $M,N,T$ be fixed. Let $P$ be on a fixed (red) line $\ell$ and let $X$ and $Y$ be an ortogonal projections of $P$ on line $MT$ and $TN$. Then the map $X\longmapsto Y$ is a spiral similarity with a center at point $F$ which is an intersection point of circle $PXY$ with $\ell$.
Proof: Since $\angle PFT = \angle PYT =90^{\circ}$ we see that $F$ is a fixed point. Now since $$\angle YXF = \angle YTF =\angle NTF = {\rm fixed \;\; angle}$$ and $$\angle YFX = \angle YTX =\angle NTM = {\rm fixed \;\; angle}$$ the triangle $XYF$ has the same angles for all $P$ so the map $X\longmapsto Y$ is a spiral similarity with rotational angle $\angle MTN$ and center at $F$.
Lemma 2: Say $Z$ is a midpoint of $XY$ from the previous lemma. Then the map $X\longmapsto Z $ is also a spiral similarity (different one) with the same center.
Idea how to finish: Clearly we have a spiral similarity $S_1$ which takes $X\mapsto Y$ and a spiral similarity $S_2$ which takes $Y\mapsto Z$.
So we have $$X\stackrel{S_1}{\longmapsto}Y \stackrel{S_2}{\longmapsto}Z$$ Now take another $X',Y',Z'$:
$$X'\stackrel{S_1}{\longmapsto}Y' \stackrel{S_2}{\longmapsto}Z'$$
I would like to show that there is a spiral similarity which takes $X$ to $X'$, $Y$ to $Y'$ and $Z$ to $Z'$ and this would prove the statement.
Clearly there is a spiral similarity that takes $X$ to $X'$ and $Y$ to $Y'$ induced by $S_1$, but I don't know how to show that it takes also $Z$ to $Z'$.
Actualy, this last claim is not quite true. I know that if $S_1$ and $S_2$ have the same center then we are done, and this is the thing I'm trying to figure out.
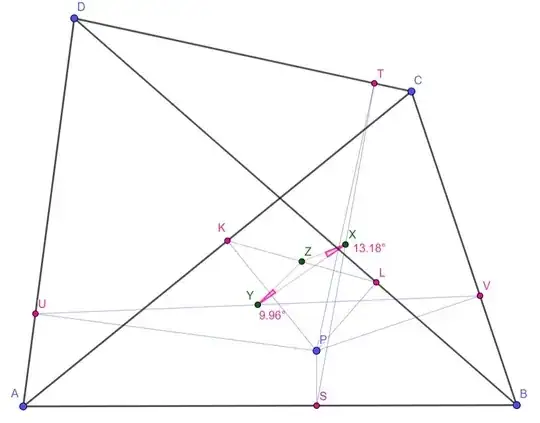
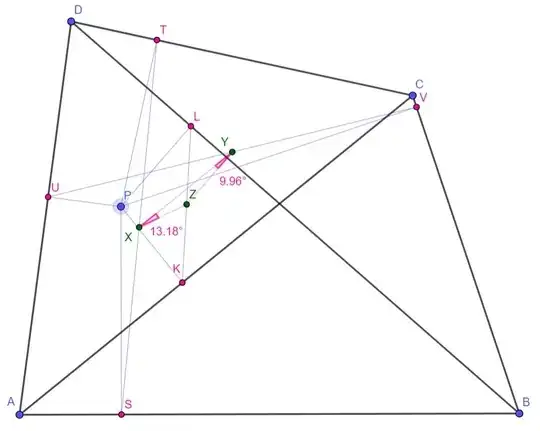
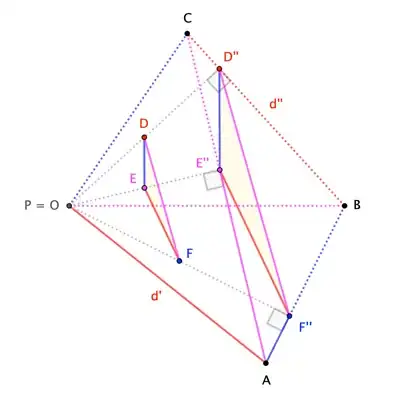
Following is an algebraic proof of the statement. To make the algebra manageable. We will choose a coordinate system where $A$ is the origin and identify the euclidean plane with the complex plane.
Let $p, z_1,z_2,z_3, u_1, v_1, w_1, w_2, w_3$ be the complex numbers corresponds to $P, B,C,D,S,T,X,Z,Y$ respectively.
Any line $\ell \subset \mathbb{C}$ can be represented by a pair of complex number, a point $q \in \ell$ and a $t$ for its direction. Points on $\ell$ has the form $q + \lambda t$ for some real $\lambda$. In order for this point to be the projection of $p$ on $\ell$, we need
$$\Re( ( q + \lambda t - p )\bar{t}) = 0\quad\implies\quad\lambda = \frac{\Re((p - q)\bar{t})}{t\bar{t}} $$ The projection of $p$ on line $\ell$, let call it $\pi_\ell(p)$, will be given by the formula
$$\pi_{\ell}(p) = q + \frac{(p-q)\bar{t} + (\bar{p}-\bar{q})t}{2\bar{t}} = \frac{q+p}{2} +\frac12(\bar{p} - \bar{q})\frac{t}{\bar{t}}\tag{*1a}$$
In the special case that $q = 0$, this reduces to $$\pi_{\ell}(p) = \frac{p}{2} + \frac12\bar{p}\frac{t}{\bar{t}}\tag{*1b}$$
Apply $(*1b)$ and $(*1a)$ to $S$ and $T$, we get
$$u_1 = \frac{p}{2} + \frac12\bar{p}\frac{z_1}{\bar{z}_1} \quad\text{ and }\quad v_1 = \frac{p + z_2}{2} + \frac12(\bar{p} - \bar{z}_2)\frac{z_2 - z_3}{\bar{z}_2 - \bar{z}_3} $$ Combine them and simplify, we get $$ w_1 = \frac{u_1+v_1}{2} = \frac{p}{2} + \frac14\bar{p} \underbrace{\left(\frac{z_1}{\bar{z}_1} + \frac{z_2-z_3}{\bar{z}_2 - \bar{z}_3}\right)}_{A_1} + \frac14 \underbrace{\left(\frac{z_3\bar{z}_2 - z_2\bar{z}_3}{\bar{z}_2 - \bar{z}_3}\right)}_{B_1}$$ Let's call the two coefficients in parentheses as $A_1$ and $B_1$. By similar argument, we can derive corresponding formula for $w_2$ and $w_3$. In general, we have
$$w_i = \frac{p}{2} + \frac14\bar{p} A_i + \frac14 B_i \quad\text{ where }\quad \begin{cases} \displaystyle\;A_i = \frac{z_i}{\bar{z}_i} + \frac{z_j-z_k}{\bar{z}_j - \bar{z}_k}\\ \displaystyle\;B_i = \frac{z_k\bar{z}_j - z_j\bar{z}_k}{\bar{z}_j-\bar{z}_k} \end{cases} $$ for $(i,j,k)$ running over cyclic permutations of $(1,2,3)$.
Given any two triangle $M$, $N$ with vertices $m_1,m_2,m_3$ and $n_1,n_2,n_3$. They are similar (with matching angles) if they have the same cross-ratio
$$\frac{m_3-m_1}{m_2-m_1} = \frac{n_3-n_1}{n_2 - n_1}$$
In order for the angles of triangle $XYZ$ to be independent of $P$, we need the cross ratio
$$\frac{w_3 - w_1}{w_2-w_1} = \frac{(A_3 - A_1)\bar{p} + (B_3 - B_1)}{(A_2-A_1)\bar{p} + (B_2-B_1)}$$ to be independent of $p$. This is equivalent to
$$\frac{A_3-A_1}{A_2-A_1} = \frac{B_3-B_1}{B_2-B_1} \iff \left|\begin{matrix}A_3 - A_1 & B_3 - B_1 \\ A_2 - A_1 & B_2 - B_1\end{matrix}\right| = 0$$ At the end, it comes down whether following complicated determinant evaluates to zero $$ \left|\large\begin{matrix} 1 & \frac{z_1}{\bar{z}_1} + \frac{z_2-z_3}{\bar{z}_2 - \bar{z}_3} & \frac{z_3\bar{z}_2 - z_2\bar{z}_3}{\bar{z}_2 - \bar{z}_3}\\ 1 & \frac{z_2}{\bar{z}_2} + \frac{z_3-z_1}{\bar{z}_3 - \bar{z}_1} & \frac{z_1\bar{z}_3 - z_3\bar{z}_1}{\bar{z}_3 - \bar{z}_1} \\ 1 & \frac{z_3}{\bar{z}_3} + \frac{z_1-z_2}{\bar{z}_1 - \bar{z}_2} & \frac{z_2\bar{z}_1 - z_1\bar{z}_2}{\bar{z}_1 - \bar{z}_2} \\ \end{matrix}\right| \stackrel{?}{=} 0 $$ If one multiply first row by $\bar{z}_1(\bar{z}_2 - \bar{z}_3)$, second row by $\bar{z}_2(\bar{z}_3 - \bar{z}_1)$ third row by $\bar{z}_3(\bar{z}_1 - \bar{z}_2)$ and sum them together, one obtain an zero row! This means above determinant vanishes and the cross-ratio $\frac{w_3 - w_1}{w_2-w_1}$ is independent of $p$.
This verify the angles in $\triangle XYZ$ doesn't depend on location of $P$.
With help of an CAS, one also obtain
$$\frac{w_3-w_1}{w_2-w_1} = \frac{A_3-A_1}{A_2-A_1} = \frac{B_3-B_1}{B_2-B1} = \frac{(\bar{z}_3 - \bar{z}_1)\bar{z}_2}{(\bar{z}_2-\bar{z}_1)\bar{z}_3}$$
The last expression is complex conjugate of a cross-ratio of the 4 numbers $(0,z_1,z_2,z_3)$. With this, we can deduce the angles of $\triangle XYZ$ from the angles among the sides/diagonals of quadrilateral $ABCD$.
As an example, in the configuration below, we have
$$\angle ZXY (\approx 13.97^\circ) = \angle CAD (\approx 46.14^\circ) - \angle CBD (\approx 32.17^\circ)$$
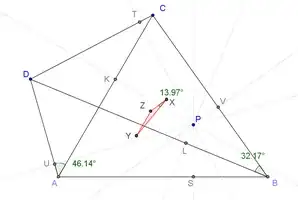
Please note that when quadrilateral $ABCD$ is cyclic, $\angle CAD = \angle CBD$. In such cases, triangle $XYZ$ degenerate into a line segment (as first pointed out by @g.kov in comment).
I hope this can inspire someone to discover a more geometric proof of this (in particular, above relations among the angles).
Radically changing the naming conventions, let $\square OABC$ be the quadrilateral, with $P$ arbitrary.
Define $$d^\prime\, := |OA| \qquad e^\prime\, := |OB| \qquad f^\prime\, := |OC|$$ $$d^{\prime\prime} := |BC| \qquad e^{\prime\prime} := |CA| \qquad f^{\prime\prime} := |AB|$$ Let $D^\prime$ and $D^{\prime\prime}$ be the projections of $P$ onto the respective (extensions of the) segments of length $d^{\prime}$ and $d^{\prime\prime}$; let $D$ be the midpoint of $\overline{D^\prime D^{\prime\prime}}$. Likewise for $E^\prime$, $E^{\prime\prime}$, $E$ and $F^{\prime}$, $F^{\prime\prime}$, $F$. Thus, $\triangle DEF$ is our triangle of interest. Finally, define $$d := |EF| \qquad e := |FD| \qquad f := |DE|$$
I claim the following:
Claim. $$d:e:f \;=\; d^\prime d^{\prime\prime}:e^\prime e^{\prime\prime} : f^\prime f^{\prime\prime} \tag{$\star$}$$
Since the right-hand-side of $(\star)$ is independent of $P$, the shape of $\triangle DEF$ is also independent of $P$. $\square$
Aside. Recall @g.kov's observation that, when $\square OABC$ is cyclic, $\triangle DEF$ degenerates to a line segment. This fact is equivalent to Ptolemy's Theorem: $$\square OABC \;\text{is cyclic} \;\iff\; d^\prime d^{\prime\prime}+f^\prime f^{\prime\prime}=e^\prime e^{\prime\prime} \qquad\left(\;\iff d+f=e\;\right)$$
Proof of Claim. Well ... I after much trying, I haven't (yet) found an approach that makes the final result "obvious". Since @OldBoy's setup is not too dissimilar from mine, I won't bother TeX-ing up my work; rather, I invite the reader to use @OldBoy's solution, but to compute simply the (squared) side-lengths (instead of the cosines) via dotProd[x-y, x-y], dotProd[y-z, y-z], and dotProd[z-x, z-x] and observe that they satisfy the (squared) equivalent of proportion $(\star)$.
I do have an argument to show that $(\star)$ is the key proportion in this scenario. (Perhaps awareness of this will inspire more-straightforward demonstrations of the target property.)
Sub-Claim. If (!!!) the shape of $\triangle DEF$ is independent of $P$, then $(\star)$ holds.
Proof of Sub-Claim. We need only consider the special case of $P=O$:
Since $D^\prime$, $E^\prime$, $F^\prime$ all coincide at $O$, we see that $\triangle DEF$ is a dilation of $\triangle D^{\prime\prime}E^{\prime\prime}F^{\prime\prime}$, with center $O$ and scale factor $1/2$. Thus, if we can show that the larger triangle exhibits the proportion in $(\star)$, we'll be done.
Consider $\overline{E^{\prime\prime}F^{\prime\prime}}$. From its position in $\triangle AE^{\prime\prime}F^{\prime\prime}$, we can compute its length via the Law of Cosines:
$$|E^{\prime\prime}F^{\prime\prime}|^2 = |AE^{\prime\prime}|^2 + |AF^{\prime\prime}|^2-2|AE^{\prime\prime}||AF^{\prime\prime}|\cos \angle BAC \tag{1}$$ But, from right triangles $\triangle OAE^{\prime\prime}$ and $\triangle OAF^{\prime\prime}$, we also have $$|AE^{\prime\prime}| = d^\prime \cos\angle OAC \qquad |AF^{\prime\prime}| = d^\prime \cos\angle OAB \tag{2}$$ Consequently, since $\angle BAC = \angle OAB - \angle OAC$, $(1)$ simplifies to $$|E^{\prime\prime}F^{\prime\prime}| = d^\prime \sin\angle BAC = \frac{d^\prime d^{\prime\prime}}{2r} \tag{3}$$ where the last equality, introducing the circumradius $r$ of $\triangle ABC$, follows from the Law of Sines. Likewise, we have $$|F^{\prime\prime}D^{\prime\prime}| = \frac{e^\prime e^{\prime\prime}}{2r} \qquad |D^{\prime\prime}E^{\prime\prime}| = \frac{f^\prime f^{\prime\prime}}{2r} \tag{4}$$ from which $(\star)$ follows. $\square$
Aside. The relation $\angle BAC = \angle OAB - \angle OAC$ that drives the simplification in $(2)$ relies on the flatness of the figure. That is, $(\star)$ does not hold if we interpret $OABC$ as a tetrahedron.
