I've been playing around with the following integral and was wondering if it can be generalised to any Real $n$. Does anyone know of any methods to approach this one?
$$ I = \int_{0}^{\infty} x^n \cos(x)\:dx $$
Asked
Active
Viewed 903 times
0
-
1The integral converges when $n\in(-1,0)$. – Tianlalu Nov 11 '18 at 04:13
-
What test(s) can we use to determine convergence? – Nov 11 '18 at 04:15
-
1Split up $I =\int_0^1+\int_1^\infty$, the first integral converges by comparison test (with $\int \frac1{x^p}$); perform IBP on the second integral, it also converges by the same test. – Tianlalu Nov 11 '18 at 04:28
-
You can use the same method employed in this answer by writing series of $\cos$ and then substituting $x^2=t$ we can then use Ramanujan's Master Theorem to arrive at the result needed. – Rohan Shinde Nov 11 '18 at 12:47
4 Answers
1
We could find its exact value via complex analysis.
Claim (generalization): $\forall \alpha\in(0,1)$,$\kappa\ge0,\lambda\in\Bbb R$, $$\int_0^\infty x^{\alpha-1}e^{-\kappa x}\cos \lambda x~\mathrm dx=\frac{\Gamma(\alpha)}{(\kappa^2+\lambda^2)^{\alpha/2}}\cos\left(\alpha \arctan\frac{\lambda}{\kappa}\right).$$
Proof:
Let $r=\sqrt{\kappa^2+\lambda^2},\gamma=\arctan(\lambda/\kappa)$, then $\kappa+i\lambda=re^{i\gamma}$,$-\pi/2<\gamma<\pi/2$. Consider the complex integral
\begin{align*}
\oint_Cz^{\alpha-1}e^{-rz}~\mathrm dz, \tag{1}
\end{align*}
where $C$ is the sector contour shown as below:
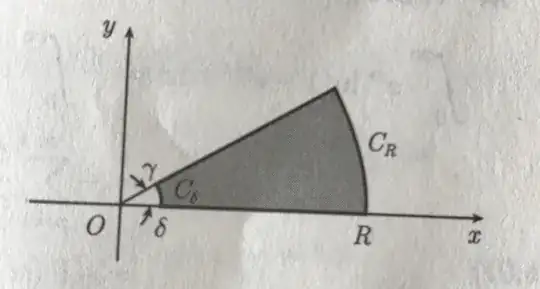We have
\begin{align*}
\oint_Cz^{\alpha-1}e^{-rz}~\mathrm dz=&\int_\delta^R x^{\alpha-1}e^{-rz}~\mathrm dz+\int_{C_R} x^{\alpha-1}e^{-rz}~\mathrm dz\\
&+\int_R^\delta (\rho e^{i\gamma})^{\alpha-1}e^{-r\rho e^{i\gamma}}e^{i\gamma}~\mathrm d \rho+\int_{C_\delta} x^{\alpha-1}e^{-rz}~\mathrm dz=0. \tag{2}
\end{align*}
Simply we can show
\begin{align*}
\lim_{\delta\to 0}\int_{C_\delta} x^{\alpha-1}e^{-rz}~\mathrm dz=0,\qquad \lim_{R\to \infty}\int_{C_R} x^{\alpha-1}e^{-rz}~\mathrm dz=0,\tag{3}
\end{align*}
therefore,
\begin{align*}
\int_0^\infty x^{\alpha-1}e^{-rx}~\mathrm dx=e^{i\gamma\alpha}\int_0^\infty x^{\alpha-1}e^{-rxe^{i\gamma}}~\mathrm dx,\tag{4}
\end{align*}
implies
\begin{align*}
\int_0^\infty x^{\alpha-1}e^{-rxe^{i\gamma}}~\mathrm dx=e^{i\gamma\alpha}\frac{\Gamma(\alpha)}{r^\alpha}.\tag{5}
\end{align*}
By comparing real part of $(5)$, the claim is established.
By comparing imaginary part of $(5)$,
$$\int_0^\infty x^{\alpha-1}e^{-\kappa x}\sin \lambda x~\mathrm dx=\frac{\Gamma(\alpha)}{(\kappa^2+\lambda^2)^{\alpha/2}}\sin\left(\alpha \arctan\frac{\lambda}{\kappa}\right).$$
Tianlalu
- 5,387
-
1In your case: $n=\alpha-1,\kappa=0,\lambda=1$, so $$\int_0^\infty x^n\cos x~\mathrm dx=-\Gamma(n+1)\sin\left(\frac{n\pi}{2}\right).$$ – Tianlalu Nov 11 '18 at 05:23
0
As $\cos(x) = \Re\left[ e^{-ix}\right]$, we arrive at
$$ I = \Re \left[\int_{0}^{\infty} x^n e^{-ix} \right] $$
Applying a change of variable $u = ix$ we arrive at,
\begin{align} I &= \Re\left[\int_{0}^{\infty} \left(\frac{u}{i}\right)^n e^{-u} \: \frac{1}{i}\:du\right] \\ &= \Re\left[ \left(\frac{1}{i}\right)^{n + 1}\int_{0}^{i\infty} u^ne^{-u} \:du\right] \end{align}
-
1you forget to change the limits of integration. If $x=\infty$ then $u=i\infty$, so the integral is not the gamma function – Nov 11 '18 at 03:58
-
-
0
Well in order to solve that kind of integrals you may arrive this problem by IBP or if you had the knowledge about complex variable doing with the elementary tools of the residual theorem.
You can check: Computing the indefinite integral $\int x^n \sin x\,dx$ and: indefinite integral of $x^n\sin(x)$
Hope that those links help!
0
The integrals you are trying to compute doesn't converge for $m\ge 1$. Note that
$$\left|\int_0^{2\pi n+\pi/4} x^m\cos(x)\, dx-\int_0^{2\pi n}x^m\cos(x)\, dx\right|=\left|\int_{2\pi n}^{2\pi n+\pi/4}x^m\cos(x)\, dx\right|\\=\left|\int_0^{\pi/4}(2\pi n+x)^m\cos(x)\, dx\right|\ge\frac{\sqrt 2}2\int_0^{\pi/4}(2\pi n+x)^m\, dx\ge\frac{\pi\sqrt 2}8(2\pi n)^m$$
Hence the sequence of integrals $(I_n)$ defined by
$$I_n:=\int_0^{a_n}x^m\cos(x)\, dx,\quad a_n:=\begin{cases}2\pi n,& n\text{ is even }\\2\pi(n-1)+\pi/4,&n\text{ is odd }\end{cases}$$
is not Cauchy, so the improper integral $\int_0^\infty x^m\cos(x)\, dx$ doesn't converge for $m\ge 1$.