a Unique Minimum Euclidean distance between point and hyperplane?

Question

$$f : x_{1}+...+x_{n}=s $$ $f$ is an n dimensional hyperplane and $x_{1},...,x_{n}$ are elements of a vector X.

All the elements of X have inequality constraints which are given below.

$$L_{1} \leq x_{1} \leq B_{1}$$

$$L_{2} \leq x_{2} \leq B_{2}$$

$$...$$

$$L_{n} \leq x_{n} \leq B_{n}$$

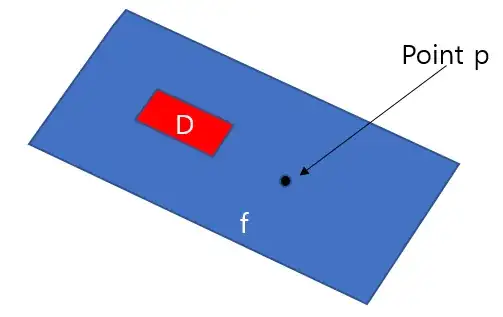
Let's say there is a domain $D$ made by $f$ and the given inequality constraints.

(Assume that $D$ must exist.)

Also, there is a point $P$ on the $f$ but not in the domain $D$.

Here, my assumption is :

"There is a unique Minimum Euclidean distance between point $P$ and domain $D$."

I'm convinced that my assumption is true but have no idea how to prove this.

Any ideas?

Thanks.

M.Kim

Answer 1

Your conjecture is correct. I'll give details below, and hope that they're at more or less the appropriate level of detail for you. If not, you need to go read up on compactness, convexity, the Heine-Borel Theorem, and the Bolzano-Weierstrass theorem. I know that's a lot, but it's all good stuff!

Renaming: I'm going to call your domain $Q$ (to avoid confusion with $d$, which I use for distance) and call the test-point $p$, reserving upper-case for sets. I'm assuming henceforth that your "rectangular" constraints don't contradict each other (i.e., you're not saying $x_1 < 3$ and $x_1 > 5$, for instance) so that $Q$ is nonempty.

1. $Q$ is closed and bounded; this is (by the Heine Borel Theorem) the same as "compact." And compact sets have many nice properties, which books in topology or introductions to real analysis will tell you about.

2. Let $S = \{ d(p, q) \mid q \in Q\}$. Then $S$ is a nonempty set of nonnegative real numbers, hence has a lower bound. (For instance, every element of $S$ is greater than or equal to $0$.) It therefore has a greatest lower bound, $b$. So far all we know is that $b$ is at least as big as $0$.

3. Because we're assuming that $p \notin Q$, I can now show that $b > 0$. Suppose not, i.e., suppose that $b = 0$ Then for every integer $n$, there must be a point $q_n$ with $d(p, q_n) < 1/n$. [Why? Well, suppose that for $n = 20$, there's no such point. That means that the distance from $p$ to every point of $q$ is at least $1/20$, hence $b \ge 1/20$.] The sequence $q_1, q_2, \ldots$ converges to $p$. But a wonderful property of closed sets is that if you have a convergent sequence in a closed set (like $Q$), then the limit of that sequence is also in $Q$. So this would imply that $p$, being the limit, is in $Q$, which is a contradiction. So the assumption that $b = 0$ is false, and we know that $b > 0$.

4. There's at least one point $c \in Q$ with $d(c, p) = b$. Reason: for each integer $n$, pick a point $r_n \in Q$ with $d(p, r_n) < b + \frac{1}{n}$ (by the same sort of reasoning as in step 3). We don't know that the sequence $r_1, r_2, \ldots$ has a limit, alas. But a nice property of compact sets is that they're bounded, so the sequence $\{r_i\}$ is bounded, and hence has a convergent subsequence (that's the Bolzano-Weierstrass theorem). Let's call the limit of that subsequence $c$. Then it's clear that (because "distance" is a continuous function of its arguments) that $d(p, c) = b$.

5. Suppose that there are two distinct points $c, c'$ in $Q$ with $d(c, p) = d(c', p) = b$. Then because $Q$ is not only closed and bounded, but convex, every point on the line segment from $c$ to $c'$ is also in $Q$. That line segment $L$ is just $$L = \{(1-t)c + tc' \mid 0 \le t \le 1 \}.$$ And we can compute the (squared) distance from points along that segment to the point $p$: \begin{align} d( (1-t)c + tc', p)^2 & = [(1-t)c + tc' - p ] \cdot [(1-t)c + tc' - p ] \\ & = [(c - p) + t(c'- c) ] \cdot [(c - p) + t(c'- c) ] \end{align} Let $h = c - p \ne 0$, and $v = c' - c \ne 0$. (The vector $v$ is nonzero because the points are distinct. Can you say why $h$ is nonzero?) Then we can continue: \begin{align} d( (1-t)c + tc', p)^2 & = [h + tv ] \cdot [h + tv ] \\ & = h\cdot h + 2t (h \cdot v) + t^2 (v \cdot v). \end{align} This is a quadratic in $t$ with positive coefficient for $t^2$, hence its graph is an upwards-facing parabola. We know the values at $ t= 0$ and $t = 1$ are the same, and hence the value at $t = 0.5$ must be lower than the value at either end! But that means that the point $\frac{c + c'}{2}$ is closer to $p$ than either $c$ or $c'$, which contradicts the claim that $c$ and $c'$ are as close to $p$ as possible. (Note that $\frac{c + c'}{2} \in Q$ because $Q$ is convex.) This contradiction means that our initial assumption --- that there were TWO points of $Q$ that both minimized the distance to $p$ --- must have been false, hence there's a unique point whose distance to $p$ is the minimum value $b$.