4

I have a discretized 3D surface for which I want to compute piece-wise linear hat functions. I assumed these functions are of the following form:

$$\phi = ax + by + cz + d$$

with the property of $\phi_i(x_j) = \delta_{ij}$.

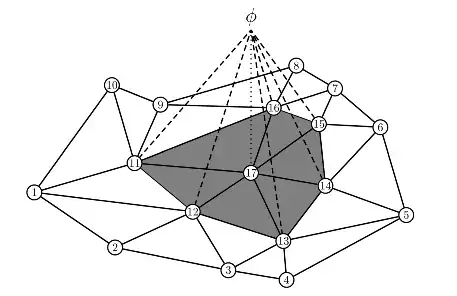
For a general 3D surface, the number of neighbors for each vertex is different, ranging from 3 to 6 or even more. For example, in the figure below, 3D vertex $i$ has 6 neighbors. This means:

$$ \phi_{17}(x_{17}) = ax_{17} + by_{17} + cz_{17} + d_{17} = 1,\\ \phi_{17}(x_{11}) = ax_{11} + by_{11} + cz_{11} + d_{11} = 0,\\ \phi_{17}(x_{12}) = ax_{12} + by_{12} + cz_{12} + d_{12} = 0,\\ \phi_{17}(x_{13}) = ax_{13} + by_{13} + cz_{13} + d_{13} = 0,\\ \phi_{17}(x_{14}) = ax_{14} + by_{14} + cz_{14} + d_{14} = 0,\\ \phi_{17}(x_{15}) = ax_{15} + by_{15} + cz_{15} + d_{15} = 0,\\ \phi_{17}(x_{16}) = ax_{16} + by_{16} + cz_{16} + d_{16} = 0.\\ $$

enter image description here

The system of equations for vertex 17 is overdetermined (7 equations and 4 unknowns) and not necessarily lead to a set of coefficients, $(a, b, c, d)$, that satisfy $\phi_i(x_j) = \delta_{ij}$.

I was wondering how piece-wise linear hat functions should be computed for such surfaces to guarantee the hat function is $1$ at vertex $i$ and $0$ at all other vertices.

shashashamti2008
  • 443
  • 2
    Your expression for $\phi$ holds only on a single triangle. The parameters $a, b, c, d$ can and will be different on each triangle since the function is only piecewise $P1$. So the problem with overdetermination is not really there. Also the surface is effectively 2D which means that there should be only 3 parameters for the hat function. – Korf Oct 24 '18 at 15:52
  • I am actually trying to understand gradient computation that is described here: https://libigl.github.io/tutorial/#gradient. I want to find the operator $\boldsymbol{G}$ in $\nabla f \approx \mathbf{G},\mathbf{f}$. Could you please let me know of your thoughts? – shashashamti2008 Oct 25 '18 at 06:54
  • 2
    What the tutorial describes is pretty much standard stuff and the tutorial itself says that $G_i = \sum\limits_{i=1}^n \nabla \phi_i(\mathbf{x})$ where $G_i$ is the row/column of $G$ and all information needed for the computation comes from the mesh. So I am afraid I am only able to suggest to read some introduction into finite element method relevant to your field. – Korf Oct 25 '18 at 16:00

1 Answers1

1

First define one triangle and interpolations as follows: $$ \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x_1 \\ y_1 \\ z_1 \end{bmatrix} + \begin{bmatrix} x_2-x_1 \\ y_2-y_1 \\ z_2-z_1 \end{bmatrix} \xi + \begin{bmatrix} x_3-x_1 \\ y_3-y_1 \\ z_3-z_1\end{bmatrix} \eta \qquad \mbox{with:} \quad \begin{cases} \xi > 0 \\ \eta > 0 \\ \xi+\eta < 1 \end{cases} $$ And quite in general: $$ \phi = \phi_1 + (\phi_2-\phi_1)\,\xi + (\phi_3-\phi_1)\,\eta $$ From this reference we infer that: $$ \begin{cases} \xi = [ (y_3 - y_1).(x - x_1) - (x_3 - x_1).(y - y_1) ] / \Delta \\ \eta = [ (x_2 - x_1).(y - y_1) - (y_2 - y_1).(x - x_1) ] / \Delta \end{cases} $$ Where $\Delta$ is twice the area of a triangle.
The Finite Element shape functions thus are, still for one triangle: $$ N_1 = 1-\xi-\eta \quad ; \quad N_2 = \xi \quad ; \quad N_3 = \eta $$ $$ x = N_1x_1+N_2x_2+N_3x_3 \\ y = N_1y_1+N_2y_2+N_3y_3 \\ z = N_1z_1+N_2z_2+N_3z_3 \\ \phi = N_1\phi_1+N_2\phi_2+N_3\phi_3 $$ Now specify for the 6 triangles in you mesh and you're done, for $\,\xi = \eta = 0\,$ eventually:

  1. $(1)\rightarrow(17) \;,\; (2)\rightarrow(11) \;,\; (3)\rightarrow(12)$
  2. $(1)\rightarrow(17) \;,\; (2)\rightarrow(12) \;,\; (3)\rightarrow(13)$
  3. $(1)\rightarrow(17) \;,\; (2)\rightarrow(13) \;,\; (3)\rightarrow(14)$
  4. $(1)\rightarrow(17) \;,\; (2)\rightarrow(14) \;,\; (3)\rightarrow(15)$
  5. $(1)\rightarrow(17) \;,\; (2)\rightarrow(15) \;,\; (3)\rightarrow(16)$
  6. $(1)\rightarrow(17) \;,\; (2)\rightarrow(16) \;,\; (3)\rightarrow(11)$
Han de Bruijn
  • 17,475