0

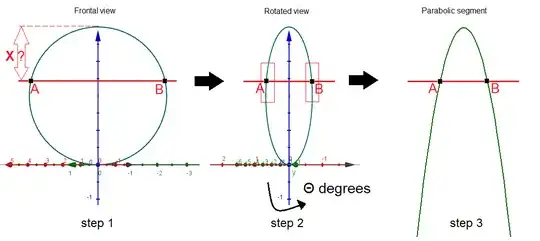
Given a known vertical, negative parabola ($y=ax^2+bx+c$ with $a$,$b$ & $c$ known parameters): how far down from the vertex of the parabola (the top) is the vertical distance, so when you "cut if off" with a horizontal line, this parabola segment is still a 3D-rotated circle segment? I refer to the following image:

enter image description here

In step $1$ a frontal view of a circle can be seen in a 3-dimensional space on $X$, $Y$ & $Z$ axes: Green is the $X$-axis, Blue the $Y$-, and red the $Z$-axis: as this is a 0 degree frontal view, $Z$ & $X$ are on the same horizontal line.

In step $2$ we now rotate this circle to the right (or left: does not matter) with a certain $\theta$ degrees. So it's still the same circle, and the same point of view, but the circle is rotated around its vertical ($Y$) axis.

In step $3$ a parabola can be seen for which the top part (above the red horizontal line $AB$) strongly resembles the top part (above the $AB$-line) of the rotated circle in the previous step. Please bear in mind that this image is an approximation.

The horizontal $AB$-line can only go so low. This is the distance $X$ in step $1$. This distance is also indicated by the rectangular boxes in point $A$ and point $B$ in step $2$: this is the point where the rotated circle on the left and on the right side stop moving away from the axis of rotation, and again start coming closer to it (sounds a bit like a derivative I guess). Could be related to conic sections also. This is the opposite of / related to this question.

MisterH
  • 357
  • 3
    I don't see what you're driving at here; surely the parabolic segment will never be identical to a segment of the ellipse shown in step 2? – Benedict Randall Shaw Oct 18 '18 at 17:10
  • As the above comment and Andrei’s answer explain, there’s basically no part of the parabola that’s elliptical. However, an interesting question to explore could be: How well can a parabola be approximated by an ellipse (or vice-versa)? – amd Oct 18 '18 at 22:49

1 Answers1

2

The rotated circle image is an ellipse. Your question is then "what piece of an ellipse is a piece of parabola?" The answer is only one point. The ellipse in your figure is $$\frac{x^2}{R^2\cos^2\theta}+\frac{(y-R)^2}{R^2}=1$$ The parabola centered on the $y$ axis has $b=0$ and $c=2R$, so the equation is $$y=ax^2+2R=0$$ These two equation have a solution $x=0, y=2R$, which is the top of the circle, and two solutions at $x=\pm\alpha$, where $\alpha$ is a function of $R$, $\theta$, and $a$. So at most your parabola intersects the rotated circle in 3 points. But in order to have a continuous segment, all three points must be identical.

Andrei
  • 39,869