(Too long for a comment)
We have
\begin{align*}
f(x)
= \sum_{k=1}^{n} \int_{0}^{\sqrt{k}} \cos x \, dx
= \int_{0}^{\infty} \left( \sum_{k=1}^{n} \mathbf{1}_{\{ x < \sqrt{k}\}} \right) \cos x \, dx.
\end{align*}
Notice that $\sum_{k=1}^{n} \mathbf{1}_{\{ x < \sqrt{k}\}} = (n - \lfloor x^2 \rfloor)_+$, where $a_+ = \max\{a, 0\}$ denotes the positive part of $a$. So
\begin{align*}
f(x)
&= \int_{0}^{\sqrt{n}} (n - \lfloor x^2 \rfloor) \cos x \, dx \\
&= \int_{0}^{\sqrt{n}} \left(n - x^2 + \frac{1}{2} \right) \cos x \, dx + \int_{0}^{\sqrt{n}} \left(x^2 - \lfloor x^2 \rfloor - \frac{1}{2} \right) \cos x \, dx
\end{align*}
The first integral is easy to evaluate:
$$ \int_{0}^{\sqrt{n}} \left(n - x^2 + \frac{1}{2} \right) \cos x \, dx
= -2\sqrt{n}\cos\sqrt{n} + \frac{5}{2}\sin\sqrt{n}. $$
To evaluate the second integral, we substitute $x^2 \mapsto x$ to write
\begin{align*}
\int_{0}^{\sqrt{n}} \left(x^2 - \lfloor x^2 \rfloor - \frac{1}{2} \right) \cos x \, dx
&= \sum_{k=0}^{n-1} \int_{0}^{1} \left(x - \frac{1}{2}\right) \frac{\cos\sqrt{x+k}}{2\sqrt{x+k}} \, dx \\
&= \sum_{k=0}^{n-1} \int_{0}^{\frac{1}{2}} x \left( \frac{\cos\sqrt{k+\frac{1}{2}+x}}{2\sqrt{k+\frac{1}{2}+x}} - \frac{\cos\sqrt{k+\frac{1}{2}-x}}{2\sqrt{k+\frac{1}{2}-x}} \right) \, dx
\end{align*}
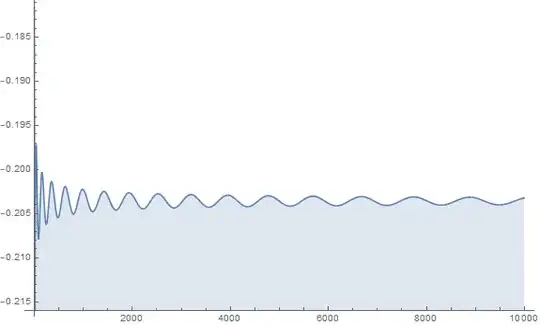
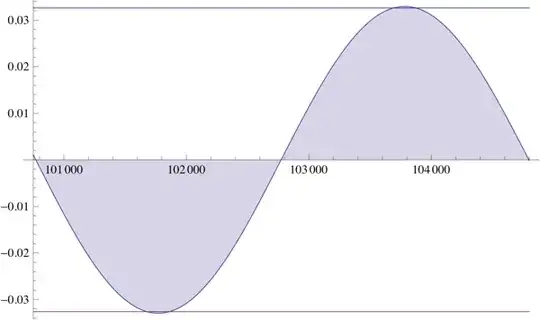
Although I cannot prove at this point, numerical evidence suggests that this integral converge as $n\to\infty$. Assuming this, it follows that
Conjecture. $c = \lim_{n\to\infty} \int_{0}^{\sqrt{n}} \left(x^2 - \lfloor x^2 \rfloor - \frac{1}{2} \right) \cos x \, dx $ converges. Consequently,
$$ f(n) = -2\sqrt{n}\cos\sqrt{n} + \frac{5}{2}\sin\sqrt{n} + c + o(1) $$
Indeed, the following figure is the plot of the difference $f(n) - \left( -2\sqrt{n}\cos\sqrt{n} + \frac{5}{2}\sin\sqrt{n} \right)$ for $n \leq 10^4$.