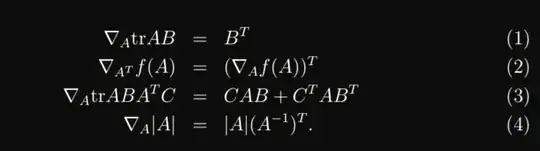0

Edit: there's another post asking the same thing, but it is not satisfactorily answered. At least not in what I believe is close to the simplest way.

Trying to prove property 3 below, in a "clean" way. That is using elementary definitions of linear algebra.

enter image description here

Attempt:

$$\nabla_A \text{tr}\left(ABA^TC\right) = \nabla_A \text{tr}\left(\left(A\right)BA^TC\right) \stackrel{(1)}{=} C^TAB^T$$

I think I'm missing some product rule stuff, but I don't see that defined anywhere in my text.

Edit2: Ahh, the second try is way wrong. Deleted it.

Rodrigo de Azevedo
  • 23,223
Zduff
  • 4,380

1 Answers1

0

We will utilize the following identities

  • Trace and Frobenius product relation $$\left\langle A, B \right\rangle={\rm tr}(A^TB) := A : B$$ or $$\left\langle A^T, B \right\rangle ={\rm tr}(AB) := A^T : B$$
  • Following properties of Trace/Frobenius product \begin{align} A : B C D &= BCD : A \\ &= A^T : (BCD)^T \\ &= B^T A D^T : C \\ &= {\text{etc.}} \cr \end{align}

We can obtain the differential first, and then the gradient. \begin{align} d \ {\rm tr }\left ( ABA^TC \right) &= d\left[A^T : BA^TC \right] \\ &= d\left[ (A^T)^T : (BA^TC)^T \right] \\ &= d\left[ A : C^T A B^T \right] \\ &= \left[ dA : C^T A B^T \right] + \left[ A : C^T \ dA \ B^T \right] \\ &= \left[ C^T A B^T : dA \right] + \left[ C A B : dA \right] \\ \end{align}

Thus, the gradient is \begin{align} \nabla_A \left[ {\rm tr }\left ( ABA^TC \right) \right] = C^T A B^T + C A B \ . \end{align}

user550103
  • 2,773