An interesting proof of $$\sum_{n=1}^\infty\left(\frac14\right)^n = \frac13$$
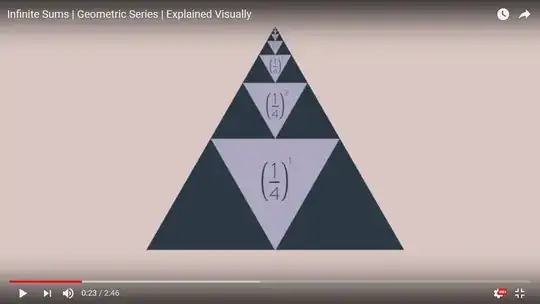
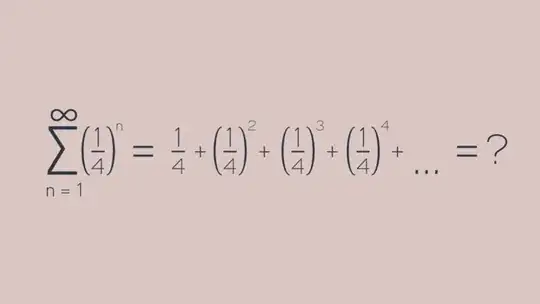 We take a triangle with unit area an divide it into four parts of equal area. We do the same process with the upper triangle an repeat this till infinity!
We take a triangle with unit area an divide it into four parts of equal area. We do the same process with the upper triangle an repeat this till infinity!
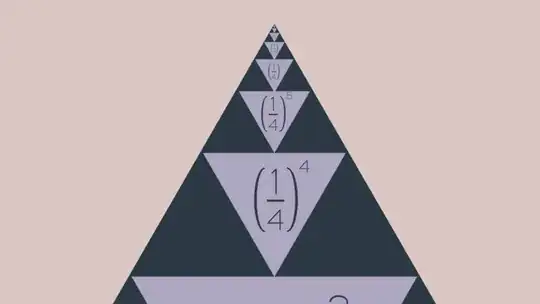
 The area of each triangle is $$\left(\frac14\right)^n$$ where $n$ is the position of triangle from bottom.
The area of each triangle is $$\left(\frac14\right)^n$$ where $n$ is the position of triangle from bottom.
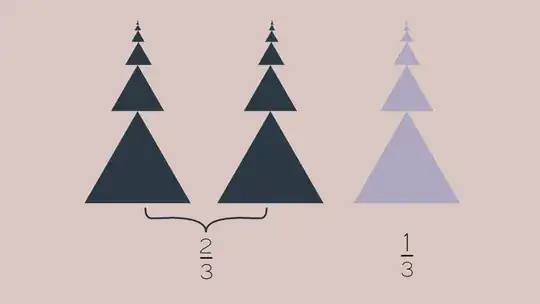
 Now we separate and rearrange the triangles:
Now we separate and rearrange the triangles:
 As the number and sizes of triangles are same, their areas will be equal. The area of the light shaded portion will be $$1/3$$
As the number and sizes of triangles are same, their areas will be equal. The area of the light shaded portion will be $$1/3$$
 $$\therefore \sum_{n=1}^\infty\left(\frac14\right)^n = \frac13$$
$$\therefore \sum_{n=1}^\infty\left(\frac14\right)^n = \frac13$$
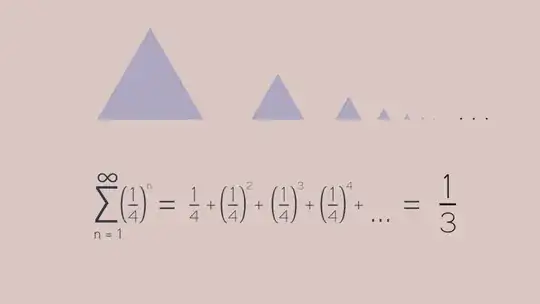 Source of the pictures- Infinite Sums | Geometric Series | Explained Visually
Source of the pictures- Infinite Sums | Geometric Series | Explained Visually
You can follow his channel at Think Twice for more such interesting visual proofs.
PS Another interesting cutting pasting proof is Area of dodecagon | Beautiful geometry | Visual mathematics
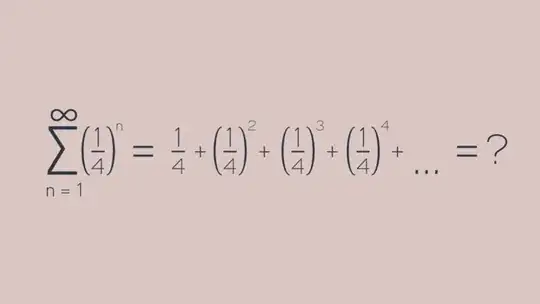 We take a triangle with unit area an divide it into four parts of equal area. We do the same process with the upper triangle an repeat this till infinity!
We take a triangle with unit area an divide it into four parts of equal area. We do the same process with the upper triangle an repeat this till infinity! The area of each triangle is
The area of each triangle is  Now we separate and rearrange the triangles:
Now we separate and rearrange the triangles: As the number and sizes of triangles are same, their areas will be equal. The area of the light shaded portion will be
As the number and sizes of triangles are same, their areas will be equal. The area of the light shaded portion will be 
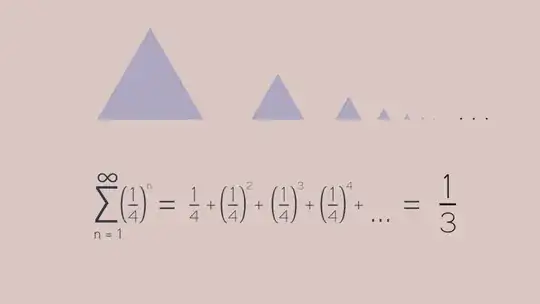 Source of the pictures-
Source of the pictures-