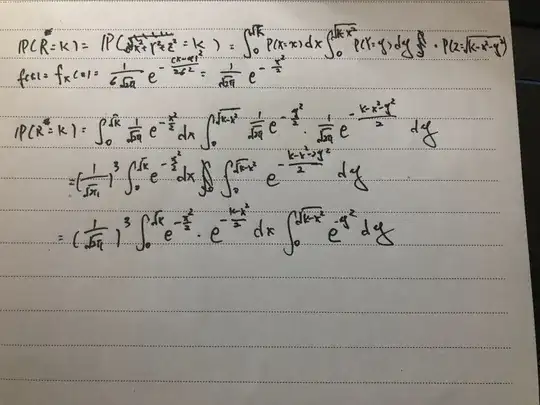
This is what I wrote, am i on the right track? and how can I solve the integral, thx
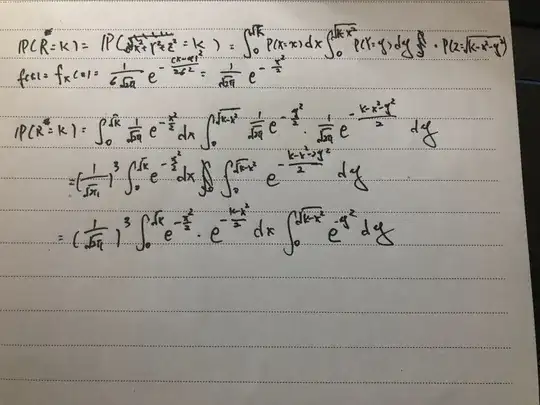
This is what I wrote, am i on the right track? and how can I solve the integral, thx
Use the Jacobian transformation method. Set
$$T_1 = X, \space \space T_2 = Y, \space \space T_3 = R= X^2 + Y^2 + Z^2$$
This can be inverted easily to find
$$X = T_1, \space \space Y = T_2, \space \space Z = \pm \sqrt{T_3 - T_1^2 - T_2^2}$$
Note that it's not one-to-one, so you need to consider the cases seperately when $Z$ is positive or negative. Hence the Jacobian $J$, which is the determinant of the matrix of partial derivatives of above inverse transformations is
$$ Z > 0: \frac{1}{2 \sqrt{T_3 - T_1^2 - T_2^2}}$$
$$ Z < 0: \frac{-1}{2 \sqrt{T_3 - T_1^2 - T_2^2}}$$
Hence, in either case, $|J| = \frac{1}{2 \sqrt{T_3 - T_1^2 - T_2^2}}$.
So the joint density function of $T_1, T_2, T_3$ is
$$f_T (t_1, t_2, t_3) = \frac{1}{2 \sqrt{T_3 - T_1^2 - T_2^2}}\left( f_{XYZ}(t_1, t_2, \sqrt{t_3 - t_1^2 - t_2^2}) + f_{XYZ}(t_1,t_2,-\sqrt{t_3 - t_1^2 - t_2^2}) \right)$$
You already know the joint density of $X,Y,Z$ (multivariate standard normal) so you can easily obtain this density by plugging in the above substitutions. In order to get the marginal distribution of $R = T_3$, all you need to do is integrate this density over the values of $T_1$ and $T_2$.
Sorry to say, but your work doesn't make much sense. You should be working with densities, not probabilities. More explicitly, using change of variables to find the distributions as it looks like the easiest route.
Being the sum of squares of independent $N(0,1)$ variables, we can directly say $$R=X^2+Y^2+Z^2\sim\chi^2_3$$
Let $$\frac{X^2}{R}=\frac{U}{U+V}$$
, where $$U=X^2\qquad \text{ and }\qquad V=Y^2+Z^2$$
Clearly $U\sim \chi^2_1$ and $V\sim \chi^2_2$, and $U,V$ are independently distributed.
Chi-square distribution is nothing but a Gamma distribution.
Using a well-known relationship between Beta and Gamma variables, we have that
$$\frac{U}{U+V}\sim \text{Beta}\left(\frac{1}{2},1\right)$$
So for a complete answer to the question it suffices to derive the distribution of $U/(U+V)$.