In Micchelli's paper Interpolation of Scattered Data: Distance Matrices and Conditionally Positive Definite Functions it mentioned that the RBF kernel $e^{-\alpha^2\|x^i-x^j\|^2/2}$ is positive definte because $$ e^{-\alpha^2\|x^i-x^j\|^2/2}=\left(2\pi\right)^{-s/2}\int_{\mathbb{R}^s}e^{i\alpha x\cdot x^i}e^{-i\alpha x\cdot x^j}e^{-\|x\|^2/2}\,dx $$ and the linear independence of $e^{ix\cdot x^1},\ldots,e^{ix\cdot x^n},x\in\mathbb{R}^s$. This looks fine with me since the kernel is a Gram matrix in this way.
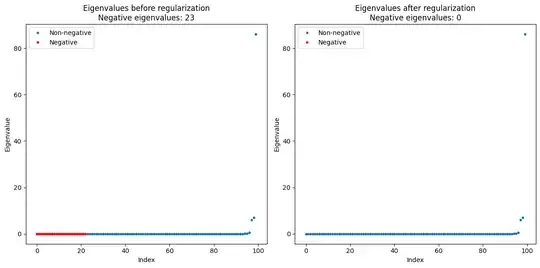
But when I calculate the RBF kernel for the s-curve data (with $\alpha^2=4$), it turns out that the eigenvalues of the kernel is not always positive. Is it a computational issue? If so, what is the robust way to calculate the eigenvalues? (I need to calculate the $\mathrm{logdet}$ actually, so robust methods for $\mathrm{logdet}$ are more welcome.)
Also, since many eigenvalues of the RBF kernel are very small, the condition number may be quite large. Can somebody give references for the condition number of RBF kernel? I've found the paper "Narcowich, F and Ward, J (1991). Norms of inverses and condition numbers of matrices associated with scattered data Journal of Approximation Theory 64: 69-94." in this page, but it's quite technical and general for me so I can't find the result specially for RBF kernel.
Thank you.