Degree of Map between Spheres

Question

Let $f: S^n \to S^n$ be a continuous morphism between $n$-spheres. One knows (for example using Freudenthal's suspension thm) that for all $n \in \mathbb{N}$ holds $\pi_n(S^n) \cong \mathbb{Z}$.

Therefore we can define the degree $deg(f) \in \mathbb{Z}$ of $f$ in following unique way such the diagram below commutates:

$$ \require{AMScd} \begin{CD} \pi_n(S^n) @>{f_*} >> \pi_n(S^n) \\ @VV \cong V @VV \cong V \\ \mathbb{Z} @>{\cdot deg(f)}>> \mathbb{Z} \end{CD} $$

Remark: the isomorphisms $\pi_n(S^n) \cong \mathbb{Z}$ are choosen compatible in the way that the fixed generator of $i_n \in \pi_n(S^n)$ is wlog in the left and right vertical maps is maped to $1$.

Therefore the map $\mathbb{Z} \xrightarrow{\text{deg(f)}} \mathbb{Z} $ is given as multiplication map $z \to deg(f) \cdot z$

Consider from now on as $f_n$ the concatenation of canonical maps

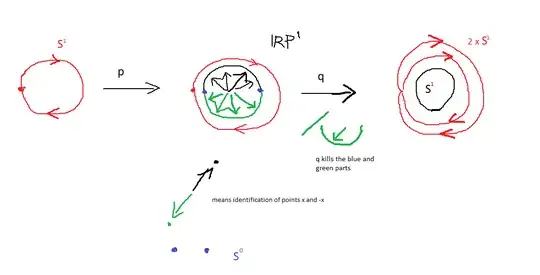
$$f_n: S^n \xrightarrow{\text{p}} \mathbb{PR}^n \xrightarrow{\text{q}} \mathbb{PR}^n/\mathbb{PR}^{n-1} \cong S^n$$

Here $p$ comes from double cover $S^n \to \mathbb{PR}^n$ and $q$ is the quotient arising from the CW / pushout structure of $\mathbb{PR}^n \cong \mathbb{PR}^{n-1} \cup_j D^n$

where $j: S^{n-1} \to \mathbb{PR}^{n-1}$ is the attatching map (the same as $p$ but for lower power $n-1$).

One can calculate using homology groups of $S^n$ and $\mathbb{PR}^n$ that

\begin{equation} deg(f_n) = \begin{cases} 2 & \text{if n odd} \\ 0 & \ \text{if n even} \end{cases} \end{equation}

My question is how one can visulize / understand intuitively that $deg(f_2) =0$ therefore that $f_2:S^2 \to S^2$ is null homotopic?

If we consider the case $f_1: S^1 \to S^1$ then one can intuitively relize that $deg(f_1) =2$ since by construction of $f_n$ and the identification $\mathbb{PR}^2 = S^1 /(x \sim -x)$ the map $f_1$ makes $S^1$ to run two times around itself.

But where is the the crux of the matter is why this argument fails for $f_2$?

Here I have drawn (please don't critizise my drawing talent :) ) the situation for n=1:

But for $S^2$ it seems since $deg(f_2)=0$ that $f_2$ can be contracted to constant map. I suppose that this has do with the properties of boundary $S^1$ but I can’t really find an intuitive argument.

Can anybody help me to visualize the intuition behind this phenomena?

Answer 1

For this post, I am thinking of $\mathbb{R}P^n$ modeled by the northern hemisphere of $S^n$ with antipodal equatorial points identified. Also, I am just going to write $f$ instead of $f_n$.

Let $N,S\subseteq S^n$ denote the (closed) northern and southern hemispheres. Let $n\in N$, $s\in S$ be the north and south pole. (For definiteness, $n = (0,0,...,0,1)$ and $s = -n$.

What is $f|_N$? Well, $p|_N$ is the identity (except for at the equator), while $q$ wraps the hemisphere all the way around the sphere. But points on the equatorial $S^{n-1}\subseteq N$ get mapped to $s$.

In other words, we may think of $f|_N$ in hyper polar coordinates as $f(\vec{\theta}, \phi) = 2\phi$. To be clear, $\phi\in [0,\pi]$ measures the angle from $(0,...,1)$ to $x\in S^{n-1}$ and $\vec{\theta} = (\theta_1,....\theta_{n-1})$ with $\theta_1\in[0,2\pi]$, but every other $\phi_i\in[0,\pi],$ is the collection of angle parameters on $S^{n-1}$. (When $n = 2$, $\vec{\theta}$ is the usual $\theta$ in spherical coordinates.)

What is $f|_S$? Well, we first use the antipodal map $a$ to move all these points into the northern hemisphere, then copy $f|_S$. So, $f|_S = f|_N \circ a$. In terms of coordinates, $a(\vec{\theta}, \phi) = (\underline{\vec{\theta}}, \pi-\phi)$ where $\underline{\vec{\theta}} = (-\theta_1, \pi-\theta_2,...,\pi-\theta_{n-1})$.

(Since the anitpodal map has degree $(-1)^{n+1}$, so far this just reproduces your proof that $\deg(f_n) = 1 + (-1)^{n+1}$.)

Thus, we may describe $f$ via $f(\vec{\theta},\phi) = \begin{cases}(\vec{\theta}, 2\phi) & \phi\in[0,\pi/2] \\ (\underline{\vec{\theta}} , 2(\pi-\phi)) & \phi\in[\pi/2,\pi] \end{cases}.$

As a sanity check, this formula clearly gives a continuous $f$ away from $\phi = \pi/2$. But $\lim_{\phi\rightarrow \pi/2^-} (\vec{\theta}, 2\phi) = s = \lim_{\phi\rightarrow \pi/2^+}(\underline{\vec{\theta}}, 2(\pi-\phi))$, so this formula describes a continuous function.

Let's assume $n $ is even. In this language, your question is to find a homotopy between $f$ and a constant map. We will write down this homotopy as a composition of two homotopies. The first homotopy uses the fact that the antipodal map $\vec{\theta}\mapsto \underline{\vec{\theta}}$ is homotopic to the identity because $S^{n-1}$ is an odd dimensional sphere. Suppose $F(\vec{\theta},t)$ is such a homotopy. (For $n=2$, you can use $F(\theta,t) = \theta + t$ with $t\in[0,\pi]$)

We claim that $f_t:=\begin{cases}(\vec{\theta}, 2\phi) & \phi\in[0,\pi/2] \\ F(\underline{\vec{\theta}},t) , 2(\pi-\phi)) & \phi\in[\pi/2,\pi] \end{cases}$ is continuous.

In fact, the argument is just as it was for $f$ above: this is clearly continuous away from $\phi = \pi/2$. And at $\phi = \pi/2$, both formulas limit to $s$, so it is continuous everywhere.

At the end of this homotopy, we get a new map $f_1 = \begin{cases}(\vec{\theta}, 2\phi) & \phi\in[0,\pi/2] \\ (\vec{\theta} , 2(\pi-\phi)) & \phi\in[\pi/2,\pi] \end{cases}.$

Intuitively, this map wraps $N$ all the way around $S^n$ with decreasing lattitude mapping to even more southern lattitudes, then wraps $S$ around the sphere with decreasing lattitude moving northern.

Let's use a final homotopy to get the constant map.

The homotopy here is $G(\vec{\theta}, \phi, t) = \begin{cases}(\vec{\theta}, 2t\phi) & \phi\in[0,\pi/2] \\ (\vec{\theta} , 2t(\pi-\phi)) & \phi\in[\pi/2,\pi] \end{cases}.$ Once again, we need to check that this is continous, and again, this is obvious away from $\phi = \pi/2$.

But when $\phi = \pi/2$, both the top and bottom map send $(\vec{\theta},\phi)$ to $(\vec{\theta}, \pi t)$, so $G$ is continuous. Finally, simply note that $G(\vec{\theta}, \phi, 0) = (\vec{\theta},0) = n$, so is constant.

Answer 2

Consider $\Bbb Z/2$-invariant cell structure on $S^n$ (two hemispheres, ..., two hemiequators, two points), call it $X$. Composition $X \to \Bbb RP^n/\Bbb RP^{n-1}$ contracts $(n-1)$-skeleton, therefore factors through $X/X_{(n-1)} = S^n \vee S^n$. Those spheres map with opposite orientations if $n$ even and with same if $n$ odd, because corresponding top cells of $X$ did so mapping into $\Bbb RP^n$.