You're given the slopes $m_1, m_2, m_3$ of the equations of the sides of a triangle and you are requested to find if this triangle is a right triangle, an obtuse angled triangle, or an acute angled triangle, without calculating any of its internal ou external angles (trigonometric values of them).
Apart from the case of a right triangle, which is pretty obvious and readily assessed, what do you do?
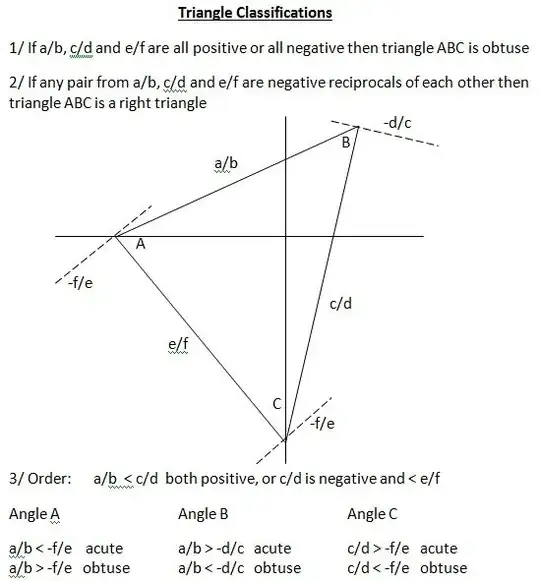
This explanation turned out longer than I thought but it's application in the example below is much shorter.
1/ Triangles with all negative or all positive gradients are obtuse triangles because a triangle with all angles less than $90$ degrees will have different signs for its gradients (perpendicular sides have negative reciprocal gradients). However, having gradients with different signs doesn't mean a triangle is necessarily acute.
2/ If two of the gradients are negative reciprocals of each other, then the triangle is a right triangle.
3/ For other triangles with different gradient signs, pick the single positive gradient or the lesser of the two positive gradients, say its line $1$ with gradient $m_1$ and determine its negative reciprocal. Now the gradients of the other $2$ sides $(2\ \text{and}\ 3)$ have to converge so there is only one way for their arrangement to work. Attaching these gradients to the ends and below line 1, the right end gradient has to be steeper than the left end gradient if both are negative. If the right hand end is steeper than the negative reciprocal of line $1$, then this is an obtuse triangle. If it isn't then the triangle is acute.
Where line $2$ and $3$ have different signs for their gradients, the positive gradient goes to the right end and the negative gradient to the left. If the left hand gradient is steeper than the negative reciprocal of line $1$, the triangle is obtuse.
If not, the last check is to determine if the angle between sides $2$ and $3$ is acute or obtuse. If the negative reciprocal of the left side is steeper than the right side, then the triangle is obtuse, if not the triangle is acute.
Example: for slopes $-1/5, 1/2\ \text{and}\ 3$
Picking the slope of $1/2$ as line $1$, it is pretty obvious that the left slope is $-1/5$ and the right slope is $3$ for the sides to converge. The negative reciprocal of $1/2$ is $-2$ whereby $-1/5$ is not steeper than $-2$ so both angles at the ends of line $1$ are acute.
Finally, the negative reciprocal of $-1/5$ is $5$ which is steeper than $3$ so the angle where sides $2$ and $3$ meet is obtuse so the triangle is obtuse.
