Given a line $ax+by=c$, the reflection transformation is
$$\begin{align}
x &\Rightarrow \frac{(b^2-a^2)x - 2aby + 2ac}{a^2+b^2}\\
y &\Rightarrow \frac{-2abx + (a^2-b^2)y + 2bc}{a^2+b^2}
\end{align}$$
We have $5x+3y=23$, so the reflection transformation here is
$$\begin{align}
x &\Rightarrow \frac{-8x-15y+115}{17} \\
y &\Rightarrow \frac{-15x+8y+69}{17}
\end{align}
$$
Before we apply this we should probably switch the hyperbola to standard form, by multiplying the whole thing by $3x$ and rearranging:
$$3xy + 2x = 20$$
We apply the transformation:
$$3\frac{-8x-15y+115}{17}\frac{-15x+8y+69}{17} + 2\frac{-8x-15y+115}{17} = 20$$
And then simplify (multiply through by $17^2=289$, expand, combine):
$$360x^2+483xy-360y^2-7103x-855y=-21935$$
Then, we can find the "function" by solving for $y$, which we can do by grouping on $y$ exponents and then using the quadratic formula:
$$(-360)y^2 + (483x-855)y + (360x^2 -7103x + 21935) = 0$$
$$\begin{align}
y&=\frac{-(483x-855)\pm\sqrt{(483x-855)^2-4(-360)(360x^2 -7103x + 21935)}}{2(-360)}\\
&=\frac{161x-285\pm17\sqrt{289x^2-4250x+12425}}{240}
\end{align}$$
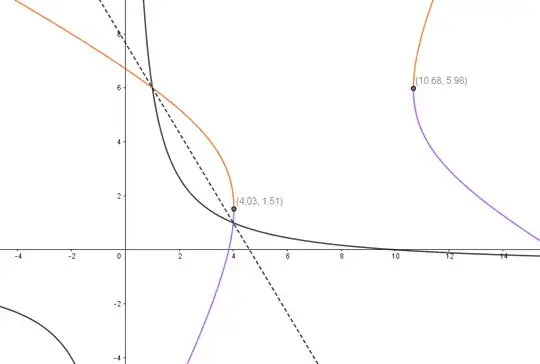
This has two parts: notice the $\pm$ in there, giving two valid $y$ values for most values of $x$.
The discriminant has roots $\frac{125\pm40\sqrt{2}}{17}$, which are the $x$ values of our branch points. As you can see in the graph below, even the small reflected part that would close the lens shape fails to be a single function.