Prove that $D$ is the incentre of the triangle $IJK$.

Question

Let $ABC$ be a triangle and $S$ its circumcircle. The points $D$, $E$, and $F$ are the feet of altitudes drawn from $A$, $B$, and $C$, respectively. The line $AD$ meets $S$ again at $K$. Let $M$ and $N$ be the midpoints of $DE$ and $DF$, respectively. If $M$ and $N$ respectively intersect $S$ at $I$ and $J$, prove that $D$ is the incentre of the triangle $IJK$.

I tried angle chasing, but failed to preceed something good (though I use scale and compass I failed to construct a proper diagram because there are so many intersections. Actually we don't have many thinks about the line joining the foots of altitudes. Please help me by giving hints or full answer

Answer 1

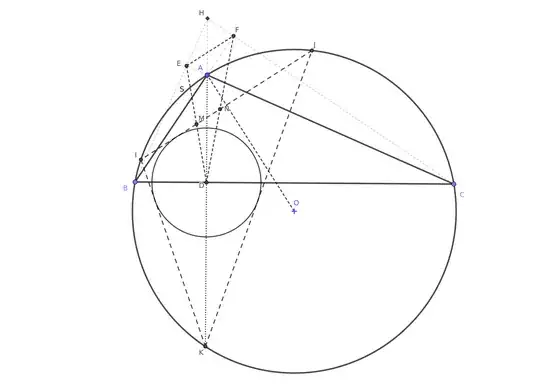
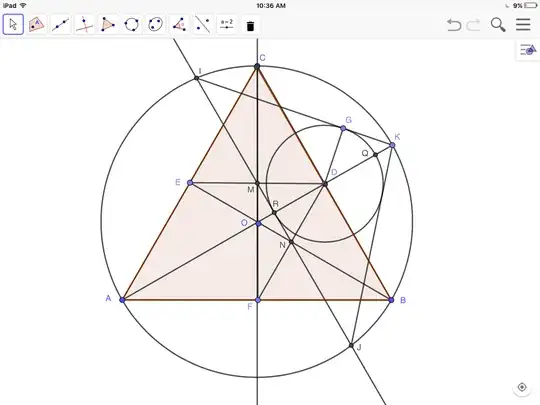
Remark: The problem as stated is not entirely correct. Only when both $\angle ABC$ and $\angle ACB$ are acute angles do we have that $D$ is the incenter of the triangle $IJK$. When $\angle ABC$ or $\angle ACB$ is a right angle, we obtain a degenerate case, where $M=E=D=B$ so that $IJ=AB$, or $N=F=D=C$ so that $IJ=AC$, respectively. If $\angle ABC>\dfrac{\pi}{2}$ or $\angle ACB>\dfrac{\pi}{2}$, then $D$ is an excenter of the triangle $IJK$. See an illustration below. (If we define $I$ and $J$ so that $MI$ and $NJ$ are disjoint, then in the case $\angle ABC>\dfrac{\pi}{2}$, $D$ is the excenter of the triangle $IJK$ opposite to $I$. On the other hand, if $\angle ACB>\dfrac{\pi}{2}$, then $D$ is the excenter of the triangle $IJK$ opposite to $J$.)

---

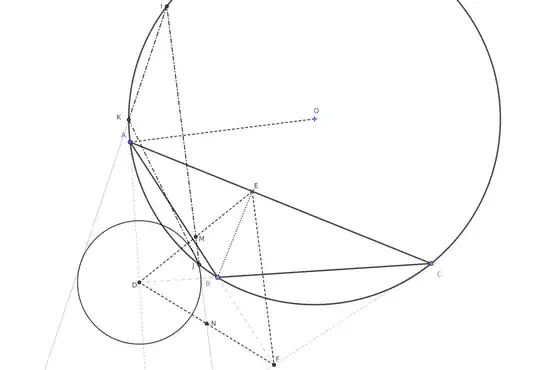
Let $R$ denote the circumradius of the triangle $ABC$. Write $\alpha$, $\beta$, and $\gamma$ for the angles $\angle BAC$, $\angle CBA$, and $\angle ACB$, respectively. In what follows, we assume that $\beta$ and $\gamma$ are in the interval $\left(0,\dfrac{\pi}{2}\right)$. First, we assume that $\alpha\in\left(0,\dfrac{\pi}{2}\right)$. Then, $$\angle DFE=\pi-2\gamma\,.$$ Thus, the distance from $D$ to $EF$ is given by $$DF\,\sin(\pi-2\gamma)=DF\,\sin(2\gamma)\,.$$ Since the triangle $ABC$ and the triangle $DBF$ are similar, we get $$DF=AC\,\left(\frac{BD}{AB}\right)=AC\,\cos(\beta)=2\,R\,\sin(\beta)\,\cos(\beta)=R\,\sin(2\beta)\,.$$ Thus, the distance from $D$ to $EF$ is $R\,\sin(2\beta)\,\sin(2\gamma)$, whence the distance from $D$ to $IJ$ is $$\rho:=\frac{1}{2}\,R\,\sin(2\beta)\,\sin(2\gamma)\,.$$

It is not difficult to see that $OA\perp EF$, whence $OA \perp IJ$. Therefore, $A$ is the midpoint of the arc $IAJ$. This shows that $$\angle DKI=\angle AKI=\angle AKJ=\angle DKJ=:\theta\,.$$ Ergo, the distance between $O$ and $EF$ is $$\begin{align}d:=OA-AE\,\sin(\beta)&=R-AB\,\left(\frac{AE}{AB}\right)\,\sin(\beta)\\&=R-\big(2\,R\,\sin(\gamma)\big)\,\cos(\alpha)\,\sin(\beta)\\&=R\big(1-2\,\cos(\alpha)\,\sin(\beta)\,\sin(\gamma)\big)\,.\end{align}$$ Thus, the distance $\delta$ between $O$ and $IJ$ is $$\begin{align}\delta=d-\rho&=R\,\Big(1-2\,\cos(\alpha)\,\sin(\beta)\,\sin(\gamma)-2\,\cos(\beta)\,\cos(\gamma)\,\sin(\beta)\,\sin(\gamma)\Big) \\ &=R\,\Big(1+2\,\big(\cos(\beta+\gamma)-\cos(\beta)\,\cos(\gamma)\big)\,\sin(\beta)\,\sin(\gamma)\Big) \\ &=R\,\Big(1-2\,\sin^2(\beta)\,\sin^2(\gamma)\Big)\,.\end{align}$$

Finally, note that $$\begin{align}DK=DH&=BD\,\cot(\gamma)=\big(AB\,\cos(\beta)\big)\,\cot(\gamma)\\&=\big(2\,R\,\sin(\gamma)\big)\,\cos(\beta)\,\cot(\gamma)\\&=2\,R\,\cos(\beta)\,\cos(\gamma)\,.\end{align}$$ Since $\delta=R\,\cos(2\,\theta)=R\,\big(1-2\,\sin^2(\theta)\big)$, we conclude that $$\sin(\theta)=\sin(\beta)\,\sin(\gamma)\,,$$ whence the distance from $D$ to $IK$ or to $JK$ is $$DK\,\sin(\theta)=DK\,\sin(\beta)\,\sin(\gamma)=2\,R\,\cos(\beta)\,\cos(\gamma)\,\sin(\beta)\,\sin(\gamma)=\rho\,.$$ Hence, $D$ is the incenter of the triangle $IJK$, with inradius $\rho=\dfrac{1}{2}\,R\,\sin(2\beta)\,\sin(2\gamma)$.

---

The case $\alpha \in\left(\dfrac{\pi}{2},\pi\right)$ can be dealt with in a similar manner. One of the differences is that $\angle DFE=2\gamma$.

Answer 2

Points $E$, $F$ lie on the circle with diameter $BC$. It follows that $\angle AEF=\angle CBA$. Let $MN$ intersect $AC$ at $X$. Since $MN \parallel EF$, we have $\angle AXM= \angle AEF$. Hence $$\angle AIC = 180^\circ -\angle CBA = 180^\circ - \angle AEF = 180^\circ -\angle AXM = \angle IXA.$$ Hence triangles $AIC, AXI$ are similar as they have the same angles. Hence $\frac{AI}{AX}=\frac{AC}{AI}$. So $AI^2=AX\cdot AC$.

On the other hand, similarly as above, $\angle DEC = \angle CBA$, hence $\angle DEC =\angle AXM$. So $MD=ME=MX$ thus $\angle AXD = 90^\circ = \angle CDA$. Hence triangles $AXD, ADC$ are similar, so $\frac{AX}{AD}=\frac{AD}{AC}$. Hence $AD^2=AX\cdot AC$.

It follows that $AD=AI$. Similarly, $AD=AJ$. Hence by trefoil lemma $D$ is the incenter od $IJK$.

Answer 3

Consider the special case where $\triangle ABC$ is equilateral, with circumradius $OC=1$.

Since $CB=\sqrt3$ and $DE=\frac{CB}{2}$, then $MD=\frac{\sqrt3}{4}$, and in $\triangle MDR$, $MR=\frac12MD=\frac{\sqrt3}{8}$, and $$RD=\sqrt{MD^2-MR^2}=\sqrt{\frac{12}{64}-\frac{3}{64}}=\frac38=.375$$

Now from $D$ make $DG\perp IK$. Since chords $AK$ and $IJ$ intersect at $R$, then$$AR\cdot RK=IR\cdot RJ$$And since $AR=\frac98$, and $RK=\frac78$, and $IR=RJ$, then$$\frac{63}{64}=IR^2$$and$$IR=\sqrt\frac{63}{64}=\frac38\sqrt7$$Hence$$\tan\angle KIR=\frac{RK}{IR}=\frac{\sqrt7}{3}=.8819$$and$$\angle KIR=\arctan .8819=41.41^o$$Therefore$$\angle GKD=\angle IKR=48.59^o$$And since$$\cos48.59^o=.6614=\frac{GK}{DK}=\frac{GK}{.5}$$then$$GK=.5\times.6614=.3307$$and$$DG=\sqrt{.5^2-.3307^2}=.375$$Therefore, the circle with radius $DR=.375$ is tangent to $IK$ at $G$. And because of the symmetry of the figure about $AK$, the same argument will show that the perpendicular from $D$ to $JK=.375$.

Hence $D$ is the incenter of $\triangle IJK$ when $\triangle ABC$ is equilateral.

So far so good, but what might be done to generalize this?