0

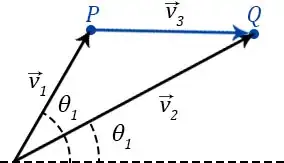
Image of vectors, points and angles.

In cartesian coordinates, we can derive the vector $\vec v_3$ by vector subtraction $\vec v_2-\vec v_1$. We then get the distance between $P$ och $Q$ by taking the absolute value of $\vec v_3$ which then is: $$\lvert \vec v_3\rvert = \lvert \vec v_2-\vec v_1 \rvert= \lvert (x_2,y_2,z_2)-(x_1,y_1,z_1) \rvert = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}$$

But how can we do this completely in cylindrical coordinates without converting to cartesian coordinates? We only have, and can only use, $\rho_1$ and $\theta_1$ for $\vec v_1$ as well as $\rho_2$ and $\theta_2$ for $\vec v_2$ in cylindrical coordinates $(\rho,\theta,z)$, where $z=0$ in this example.

Defindun
  • 315

1 Answers1

0

Your problem for $z=0$ reduces to the polar coordinate problem already answered here. $$|\vec v_3|^2=(\vec v_2-\vec v_1)\cdot(\vec v_2-\vec v_1)=|\vec v_1|^2+|\vec v_2|^2-2\vec v_2\cdot \vec v_1$$ Now using cylindrical coordinates, $|\vec v_i|^2=r_i^2+z_i^2$ and $\vec v_2\cdot \vec v_1=r_1r_2\cos(\theta_2-\theta_1)+z_1z_2$. Then the final answer will be $$|\vec v_3|^2=r_1^2+r_2^2-2r_1r_2\cos(\theta_2-\theta_1)+(z_2-z_1)^2$$

Andrei
  • 39,869
  • Yes, I've seen this solution, but isn't it based in terms of cartesian coordinates/base vectors, $\hat e_x$, $\hat e_y$ and $\hat e_z$ after all? This since, I guess, you must express a distance in constant base vectors? I'm a bit confused about how to interpret the problem I have to admit. How would it look if I want to express the solution completely in cylindrical coordinates with $\vec v_1=\rho_1 \hat e_\rho (\theta_1)$ and base vectors $\hat e_\rho$, $\hat e_\theta$, and $\hat e_z$ etc? Would that be possible? – Defindun Sep 06 '18 at 05:46
  • I did not use Cartesian coordinates. The $z$ coordinate is there in cylindrical system. The only other reference to the Cartesian system is the angle $\theta$. The issue that you have is that the basis of the cylindrical coordinate system changes with the vector, therefore equations will be more complicated. – Andrei Sep 06 '18 at 06:38
  • Okay, I see. is it possible to express the solutions with the base vectors of the cylindrical coordinates? Do you have to choose one of the vectors as the reference then or how does that work since they have different vector basis due to different angles? Thanks! – Defindun Sep 06 '18 at 06:45
  • If you choose one of the vectors as the reference, the cylindrical coordinate system is just a Cartesian system rotated with respect to the original. $\hat e_\rho$ is the new $\hat e_x$, and $\hat e_\theta$ is the new $\hat e_y$. – Andrei Sep 06 '18 at 07:19
  • Yes, that seems reasonable. So the only real applicable solution is the one you have described in your first answer above? Or are there any other solutions where "equations will be more complicated"? Thank you. – Defindun Sep 06 '18 at 07:23
  • In this case, calculating $\theta$ is relatively easy, the $z$ component is trivial ($z_2-z_1$). If you want more complicated, try to repeat the angle calculations for spherical coordinate system. – Andrei Sep 06 '18 at 08:14