How to find semi-axes length of the ellipse if four points (top ,bottom,left right) on ellipse is given( enclosing by a rectangle.) I have used this explanation but still not getting the correct orientation?
Extrema of ellipse from parametric form
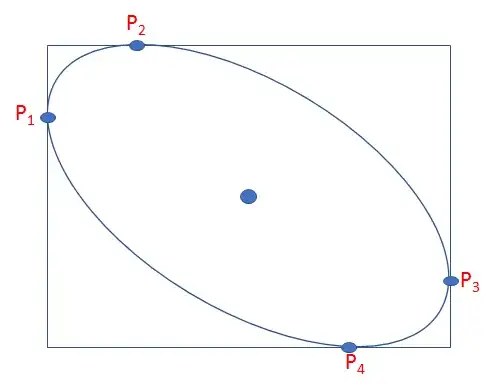
How to find semi-axes length of the ellipse if four points (top ,bottom,left right) on ellipse is given( enclosing by a rectangle.) I have used this explanation but still not getting the correct orientation?
Extrema of ellipse from parametric form

Let the equation of centered ellipse be
$$ax^2+2bxy+cy^2=1.$$
We find the $y$ extrema from $$\begin{cases}ax+by+bxy'+cyy'=0,\\y'=0.\end{cases}$$
or just
$$ax+by=0.$$ Similarly for the $x$ extrema, leading to
$$bx+cy=0.$$
As the symmetry is implicit in the equation, you have two known points, which you can plug in the first equation and the respective extremal conditions, giving an overdeterminate system of four equations in three unknowns.
But if all you know is $W,H$, you end up with an indeterminate system of four equations in five unknowns. The solution is not unique.