0

The fact that each prime number (greater than $9$) ends with one of the four digits $1,3,7,9$, allows us to classify the tens in which the primes are found according to which of these four digits, added to the tens, yields to a prime number.

For example, for the first ten we have $1 \rightarrow \{1,3,7,9\}$. In fact, $10+1$, $10+3$, $10+7$ and $10+9$ are all primes. Conversely, for the twentieth ten the association reads $20 \rightarrow \{\}$, since there are no primes between $200$ and $209$.

It is easy to see that each ten is associated to one (and only one) group of symbols, chosen among the following $16$ distinct alternatives: $\{\}$, $\{1\}$, $\{3\}$, $\{7\}$, $\{9\}$, $\{1,3\}$, $\{1,7\}$, $\{1,9\}$, $\{3,7\}$, $\{3,9\}$, $\{7,9\}$, $\{1,3,7\}$, $\{1,3,9\}$, $\{1,7,9\}$, $\{3,7,9\}$, $\{1,3,7,9\}$.

For the sake of simplicity, we can identify each of these $16$ distinct groups of symbols with a single symbol, or with a single color, as illustrated below:

enter image description here

Each of these colors represents how many prime numbers there are in one ten (and which ones). In practice, we have just split the complexity of primes into tens and colors.

The color-code is of course arbitrary, and a better choice is possible. Here I chose a gradient that ranges from no primes at all in a ten (black) to all the four possible primes in a ten (white), intentionally avoiding fancier solutions (any suggestion is welcome!).

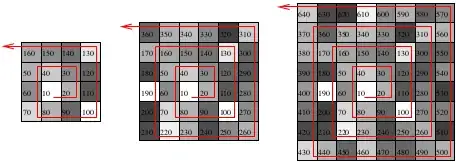
By means of this representation it is possible to build a discrete spiral (as suggested by Alex R. here) in which each tile represents one ten, and whose tiles color obeys the code illustrated before.

Here I show some examples until the ten 160, 360 and 640 (the number inside the tiles indicates here the related ten).

enter image description here

And here I present a more expanded example, until the ten 2250.

enter image description here

Finally, I present an excerpt of the upper part of the spiral ranging up to 25000 tens, apparently showing peculiar coiled, bundled super-structures, recalling fluid turbulence (click on the image to expand it).

enter image description here

(It would be great if someone could reproduce the same result with a different platform/code. See the NOTE at the bottom for technical details).

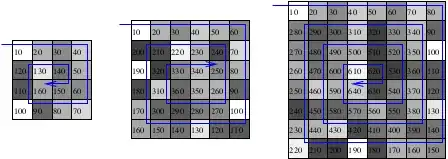
Now, the construction of the discrete spiral can be done, given a number of tens, also from outside to inside, as illustrated below

enter image description here

Let us compute the same spiral as before, up to 2250 tens:

enter image description here

And then let analyze a detail of the spiral related to 25000 tens:

enter image description here

Again, it seems that we find similar coiled super-structures as we have obtained for the spiral built starting from the center.

My question is:

How can we define/quantify the similarity of these two kinds of spirals? And, admitting that there is a similarity, where does it come from?

And, in general, which techniques are used to study this kind of data? Can we treat them as stochastic/random matrices? I would say no, but I am not sure.

A related question (still a reference request) is if somebody knows whether such approach to the study of prime number was already attempted.

EDIT: As suggested in the comments, here's the spiral of 2250 tens with random values for the tiles color-code (chosen among the 16 shades defined above):

enter image description here

and an extract of a 25000-tens spiral with random values:

enter image description here

Which brings us back to the open question.

Thanks for your comments and suggestions. Sorry for naivety, trivialities, and imprecision.

NOTE: The pictures are obtained with a combination of $\texttt{R}$, Xfig and bash. Prime numbers are calculated with the $\texttt{factorize}$ function, available within the $\texttt{R}$-package $\texttt{gmp}$.

See also this post, in which I introduce the same representation.

Community
  • 1
  • 2
    Have you, for comparison, tried generating a random string of these sixteen shades of gray and arranging them in a spiral. Does a simular turbulent pattern emerge? – John Wayland Bales Sep 02 '18 at 21:17
  • @JohnWaylandBales No, but it is a good idea. However, there are also other not-random structures (e.g. look at the left side of the second extract, there is like a straight line, unless it is an artifact). I will do it! Thanks! –  Sep 02 '18 at 21:19
  • It would bolster your case that this is not a random effect. – John Wayland Bales Sep 02 '18 at 21:20
  • @JohnWaylandBales Done! I edited the post. To me, it seems the same as the primes-spiral (just a bit whiter, as it should). This actually reinforce the motivation of the question. How can we distinguish/analyze these two kinds of data sets? –  Sep 02 '18 at 22:34
  • 1
    Instead of a random string of gray shades, it might be better to look at a string where the probability of a gray shade is related to the number of primes (0 to 4) expected in the range of 10 integers using a rough estimate from the prime number theorem. That is, for the range $[10N..10N+9]$, choose a random variate from the binomial distribution for $4$ trials with probability of success $p=2.5/(\ln 10N)$, and then choose a random shade of gray for a set with that number of $1$s in it. [Quickly corrected $0.4$ to $2.5=1/0.4$.] – Steve Kass Sep 02 '18 at 23:05
  • @SteveKass Great! I will do it! Thanks! –  Sep 02 '18 at 23:06
  • 1
    @AndreaPrunotto We tend to see a pattern even if there is none. And even if the first primes form a pattern , this pattern will amost surely eventually vanish , if we go to larger primes. Always remember : "Big primes (and numbers) are different!" – Peter Sep 06 '18 at 11:22

0 Answers0