2

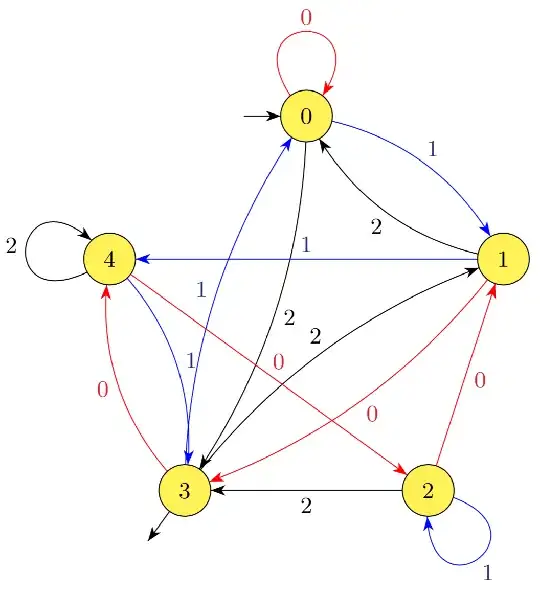
The problem:

Professor Martinez needs a state machine that will recognize certain base-$3$ numbers. It should read the digits in left-to-right order. That is, if you’ve seen number $x$ and read a new digit $d$, your new number is $3x + d$. The machine should be in a final state whenever the number read so far is congruent to $3 \pmod 5$. For efficiency, the state machine must be deterministic. Specifically, if you look at any state $s$ and any action $\text{a}$, there is exactly one edge labelled $\text{a}$ leaving state $s$. Draw a state diagram that will meet his needs, using no more than $7$ states and, if you can, no more than $5$.

I already know the graphical solution to the problem, but I'm having trouble figuring out the logic behind it. How do I know if a base $3$ number is congruent to $3 \pmod 5$? So far, I have the following algorithm:

for every digit k in number n:
    if(3k + d == 5k - 2) {
        send to final state   //is congruent to 3(mod 5)
    }
    else {
        3k = 3k + d   //updates the total value k
    }

I'm not sure how to implement this in state diagram form, since any given number can have an arbitrarily large number of digits.

Michael Hardy
  • 1
dxxg-syz35
  • 101

4 Answers4

2

This is exactly the same answer as Ross Millikan but it took me some time to prepare the corresponding picture. Here it is:

$\hskip 50pt$

J.-E. Pin
  • 42,871
1

Your states should be the remainder of the number read so far when divided by $5$. You start in state $0$ because you haven't read any digits so there is no remainder. From each state $s$ when you read $a$ you should go to state $3s+a \pmod 5$. The exception would be state $3$ which is supposed to be final, so there is no exit from there. As an example, if you are in state $1$ and read $2$ you would go to $3\cdot 1 +2 \pmod 5=0$

Ross Millikan
  • 383,099
0

I don't know anything about finite state machines.

The modular part is likely clearest using $81 \equiv 1 \pmod 5.$ That means that you can take a base 3 number with digits (all 0,1,2) abcdefghijk and split it up as abc,defg,hijk (similar to the way we put commas for 1000 except four digits at a time). Then have a mod 5 evaluation for hijk, add that for defg, add that fr the three digit abc.

If you insist on going left to right you may be talking about Horner's rule for evaluating polynomials. Whatever step you are at, add the next digit, multiply by 3, reduce mod 5. Certainly that would work as an ordinary computer program.

Will Jagy
  • 146,052
  • As far as I understood correctly the input is an infinite number of digits such as "010201212011002012...". The state machine should stop whenever the digits already read form a number that is congruent modulo 3. So in the example the machine would stop after "010". – Martin Rosenau Aug 28 '18 at 19:01
  • @MartinRosenau thank you. It seems he already has the Horner algorithm as a miniature program, and the difficulty is some sort of diagram. He should probably write a working program in some easy language, give it finite strings of digits, see if it stops correctly. The diagram may begin to appear once the mathematical process is understood. – Will Jagy Aug 28 '18 at 19:09
0

for every digit k in number n
3k = 3k + d

Do you have typing mistakes here?

Should it be for every digit d? Should it be k = 3k + d?

What exactly is k?

3k + d == 5k - 2

At least this expression definitely looks wrong to me...

... if you can, no more than 5.
... but I'm having trouble figuring out the logic behind it.

Let's say the variable i in a computer program is the ternary number already read. k is the congruence of that number modulo 5. Then our program reading the numbers and calculating the modulus would look like this:

i = 0
k = i mod 5
for each digit d in the input:
    i = 3*i + d
    k = i mod 5

We could of course change the lines in the loop:

k = (3*i + d) mod 5
i = 3*i + d

Now there are two rules of modulo calculation that we apply:

  • I) $(a+b) \mod c = ((a \mod c)+b)\mod c$
  • II) $(ab) \mod c = (a(b \mod c))\mod c$

This means:

$(3i+d)\mod 5 \overset{(I)}=\\ (((3i) \mod 5)+d)\mod 5 \overset{(II)}=\\ (((3(i \mod 5)) \mod 5)+d)\mod 5 \overset{(I)}=\\ (3(i \mod 5)+d)\mod 5$

So the content of our program now looks like this:

k = (3*(i mod 5) + d) mod 5
i = 3*i + d

And because k is nothing but i mod 5 we can replace i mod 5 by k:

i = 0
k = 0  // 0 mod 5 = 0
for each digit d in the input:
    k = (3*k + d) mod 5
    i = 3*i + d

We see that i is no longer needed to calculate k; so if we are only interested in k we can remove i:

k = 0
for each digit d in the input:
    k = (3*k + d) mod 5

The variable k can only have 5 different values: 0, 1, 2, 3 and 4.

This means that we can use a state machine having 5 states named: "k=0", "k=1", ..., "k=4".

For each of the 5 states and the 3 possible inputs (0, 1, 2) we can calculate the next state. For example we could calculate the next state after state "k=1" if d=2: (3*1+2) mod 5 = 0 so we have a transition from the state "k=1" to the state "k=0" if d=2.

The machine should be in a final state whenever the number read so far is congruent to 3 (mod 5).

... when such a number has been seen we are in state "k=3".

So by simply removing (or not drawing) the transitions leaving the state "k=3" we will stay in the state "k=3" forever when we have seen a number that is congruent 3 modulo 5.

Martin Rosenau
  • 1,293