0

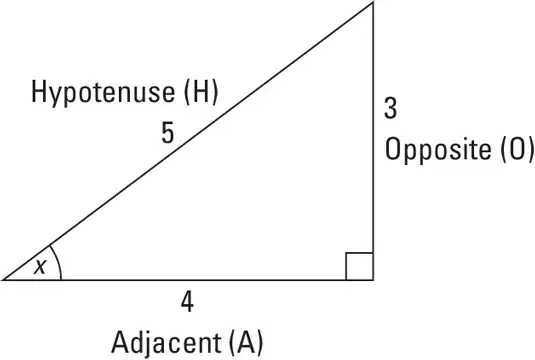
Lets say for example I have a triangle like the one below:

enter image description here

If I find x by doing

$\sin^{-1}\dfrac {3}{5}$

is the resulting number in degrees or radians? I understand that a calculator can be set to return degrees or radians, but what is this number inherently? If I have misunderstood something then please let me know.

bjcolby15
  • 4,210
Tyler S. Loeper
  • 111
  • Mostly radians, sometimes degrees. – Love Invariants Aug 27 '18 at 17:09
  • 1
    The result of your calculation is going to depend on whether your calculator is in degrees or radians. SOH CAH TOA, though, is independent of radians or degrees, because it is going the other way. – Adrian Keister Aug 27 '18 at 17:09
  • 4
    Sine of an angle is opposite length over hypotenuse, regardless of what units the angle is in. But you will need to decide what units you want to use to compute $\sin^{-1}(3/5)$ – ziggurism Aug 27 '18 at 17:10
  • 3
    The resulting number is an angle. Angles do not inherently by themselves have a preferred unit of measurement, just like how length does not have a preference for meters versus feet. How you interpret that angle depends on what you want. If you want the result to be in radians then you have an answer of about $0.643$ (rad). If you want the result to be in degrees then you have an answer of about $36.87^\circ$ – JMoravitz Aug 27 '18 at 17:11
  • It is generally preferred in the mathematical community to use radians as it makes several calculations "nicer." For example, in calculus if we interpret $\sin(x)$ and $\cos(x)$ as taking inputs in terms of amounts of radians we have the derivative of $\sin$ being $\frac{d}{dx}[\sin(x)]=\cos(x)$. However, if we want to instead interpret inputs as degrees we would instead have $\frac{d}{dx}[\sin(x)]=\frac{\pi}{180}\cos(x)$. See this question. – JMoravitz Aug 27 '18 at 17:17

1 Answers1

6

This mnemonic isn't inherently in any specific unit for measuring angles. The sine is $3/5$; that's not a convention of units, just an objective fact. Now, if you run it through an inverse sine calculator, it'll return an answer in whatever units it's designed to. Calculators typically have degree, radian and grad conventions you can switch between. And that convention is used when interpreting what angle you'd like the sine of, if you ask for it. If $\sin 30$ comes out as $0.5$, you're working in degrees. But that's all it is, a convention.

J.G.
  • 118,053