In a Cayley table, which Group axioms fail when an entry appears twice in a row or a column?
It's obviously not the Closure axiom, and after some inspection, I believe the Inverses axiom does fail.
However, I'm not so sure how to show whether or not the two other axioms fail (Identity and Associativity).
For any group property, you can always find a Cayley table where there's a duplicate entry and yet that property still holds. Here are examples for each:
Associativity can still hold. $$\begin{array}{c|cc} \times& 0 & 1 \\\hline 0 & 0 & 0\\1 & 0 & 1\end{array}$$
Identity can still hold. (Same example.) $$\begin{array}{c|cc} \times& 0 & 1 \\\hline 0 & 0 & 0\\1 & 0 & 1\end{array}$$
Inverses can still hold. (Here, $a$ and $b$ are inverses of each other.)$$\begin{array}{c|ccc} & e & a & b \\\hline e & e & a & b\\a & a & a & e \\b & b & e & a\end{array}$$
If there's a duplicate row, then $ab=ac$ for some $b\neq c$. Suppose the operator has inverses and associativity. Then we get $a^{-1}ab = a^{-1}ac$ so that $b=c$— contradicting our assumption that $b\neq c$.
So if there's a duplicate row, the operator can either be associative (as shown above), or have inverses (as shown above), but never both.
For confirmation, note that in the example tables above, #1 is associative but not invertible because of 0, and #3 is invertible but not associative because $(bb)a = aa = a$ but $b(ba) = be = b$.)
Groups can't have repeat entries. Therefore, if a table has repeat entries, it's not a group. If it's not a group, then it's not in the green region of this diagram. Visually, you can see that such a table can't be both associative and have inverses at the same time. And you can show that there exist tables with duplicate rows that belong to any other non-green region of this diagram.
If you have a monoid, an entry can appear twice in a row or a column. However, the axioms "Identity" and "Associativity" are satisfied. Suppose now that $xa = xb$ with $a \not= b$. Then $x$ cannot have an inverse, since otherwise $xa = xb$ implies $x^{-1}xa = x^{-1}xb$, that is, $a = b$.
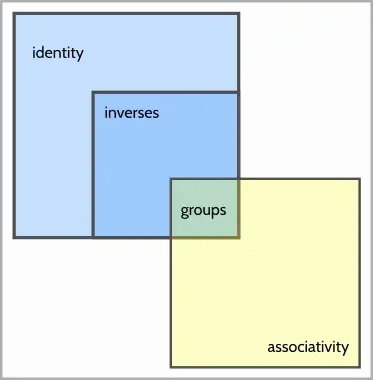
Update: The proof I gave that you can't have inverses at all assumed associativity. Out of the three properties in question (identity, inverses, associativity), you can have any combination whatsoever as long as it does not have both inverses and associativity.
This change can be made without affecting the identity, though it doesn't have to. As an example, consider the additive group $\mathbb{Z}_2$ with $1+1=1$ instead of $1+1=0$. By inspection of the 3 relevant cases, there is still an identity in this set and operation even though rows and columns have duplicated information.
That isn't mandatory. The offending definition could just as well have been $0+1=0$, with nothing else changed. One could easily verify that the resulting set and operation do not have an identity.
If there is not an identity, inverses don't exist. At least, the definitions of inverse that I'm familiar with explicitly define such a thing in terms of an identity.
If there IS an identity, inverses still don't exist. Consider (with multiplicative notation and an identity of $e$) the equation $ax=bx$ corresponding to a row with duplicates if $a\neq b$. Note that if inverses existed we would have $ae=be$, but since $e$ is the identity we have $a=b$, violating $a\neq b$.
Associativity can go either way. The object $\mathbb{Z}_2$ with $1+1=1$ is associative and even has an identity. As far as modifications to $\mathbb{Z}_2$ are concerned, there are non-associative options as well (like all additions being $0$ except $0+1=1$), but none of them have a proper identity.
With slightly more elements, we can lose associativity and retain the identity. Consider the set $\{0,1,2\}$ with $0$ as an identity, $1+1=0$, and $2+1=0$. Note that $$\begin{aligned}2+(1+1)&=2+0\\&=2\neq1\\&=0+1\\&=(2+1)+1.\end{aligned}$$ The remaining operations can be defined however you want, and this Cayley table still corresponds to a set with an identity and without associativity.
