9

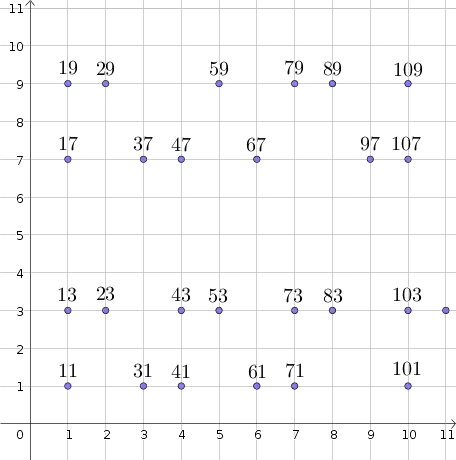
Given the series of prime numbers greater than $9$, we organize them in four rows, according to their last digit ($1,3,7$ or $9$). The column in which they are displayed is the ten to which they belong, as illustrated in the following scheme.

enter image description here

My conjecture is:

Given any two primes, it is always possible to find an ellipse whose foci coincide with the two points corresponding to the given primes in the previous representation, and passing through at least other two points, corresponding to other two primes.

Here I present some examples, where the red segments connect the two foci of each illustrative ellipse. Sorry if the picture is a bit chaotic!

enter image description here

Since I am not an expert of prime numbers, this can be an obvious result. In this case, I apologize for the trivial question. Anyway, I tried to prove this conjecture by means of the interesting observations related to this post, which is strongly related.

Thanks for your comments or suggestions, also to improve the quality and correctness of this question!

  • Just curious: why did you include euclidean-geometry and conic-sections as tags? I get that ellipses are "conic sections" and this can be a geometric question, but how will these be related in solving the problem.. – YiFan Tey Aug 21 '18 at 12:37
  • @user496634 True. I though that experts in conic-sections and geometry may have some clue that is not too strongly related to prime numbers etc. Can you suggest me better tags? Thanks! –  Aug 21 '18 at 12:40
  • 1
    What an excellent question. – Klangen Aug 22 '18 at 13:01
  • @PreservedFruit Thanks! –  Aug 22 '18 at 13:13
  • 1
    This is hardly a trivial question. A very interesting intersection of number theory and geometry. – Mr. Brooks Aug 22 '18 at 20:52
  • 1
    @Mr.Brooks Thanks. You might be interested also in these other questions, that are strongly related to this one: https://math.stackexchange.com/q/2886024/559615, https://math.stackexchange.com/q/2888522/559615 and https://math.stackexchange.com/q/2889224/559615. Hope you like them. Thanks again, Mr. Brooks. –  Aug 22 '18 at 21:25

1 Answers1

2

We just need to prove that there are two points such that the sum of each of their distances from the two focii is the same. The most obvious pair are those symmetrical with respect to the line linking the two focii, and/or its perpendicular bisector. For example, taking the primes $(3,7)$ and $(4,3)$, the primes $(1,3)$ and $(6,7)$ satisfy this condition.

The intuition is that eventually, given the infinite number of primes, one will always be able to find such pairs of numbers so that this condition is satisfied. However, I am unable to prove this, so I doubt that it is true for large primes, as prime gaps mean that it becomes increasingly unlikely that these numbers can be found.

YiFan Tey
  • 17,740
  • 4
  • 30
  • 73
  • 1
    Basically whenever you have two pairs of primes such that $p_1+q_1=p_2+q_2$ then one pair lies on an ellipse of the other, and vice versa. I reckon that for larger numbers it happens more often (see for example Goldbach's conjecture wiki). So you'd have a better chance of a counterexample with smaller primes. There are other ways to have points on an ellipse that you have to check though. Still, $11$ and $23$ looks like it could be a good candidate, or $23$ and $31$. – Jaap Scherphuis Aug 21 '18 at 15:14
  • @JaapScherphuis Thanks for your comment Jaap. I tried indeed other ways, but this is the only one that (it seems) is valid for all the couple of primes I tried, and I tried many. Other ways involved to get 5 primes on a conic, etc. but they are not as general as this one. The only other general way I found so far is here: https://math.stackexchange.com/q/2886024/559615. Thanks!! –  Aug 21 '18 at 16:41