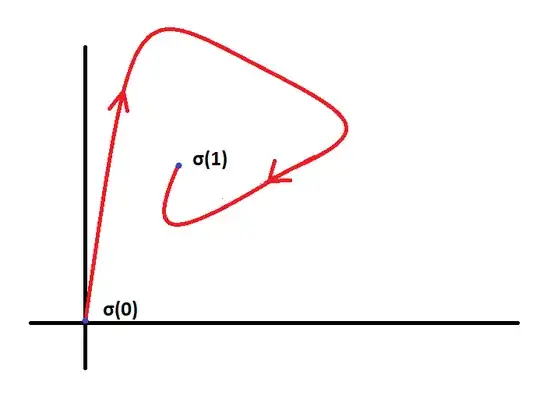
No such function is injective. In the following answer, since I'm having trouble getting pictures to my computer, I recommend following along with pencil and paper.
The primary thing to consider for this is the turning number of a smooth curve $\gamma$ - this is just the number of times its derivative $\gamma'$ circles the origin. Of note is that you have defined $\sigma$ to have turning number $1$ on the interval $[0,1]$.
Now, let's make a topological claim: Suppose we have a simple curve $\gamma$ which begins and ends on a line $\ell$ and let's suppose that $\gamma$ only intersects $\ell$ at finitely many points and does so transversally (i.e. actually crosses the line). Now, we don't know the exact value of $\gamma'$ at each intersection, but we know whether $\gamma'$ lies above or below $\ell$ at each intersection based on which direction $\gamma$ crosses the line in - which basically tells us, up to a half turn, how much $\gamma$ has rotated. As an example, here are the only four things $\gamma$ could do if it only intersects the line twice, labelled with fractional turning numbers, where $\gamma$ goes from $A$ to $B$:
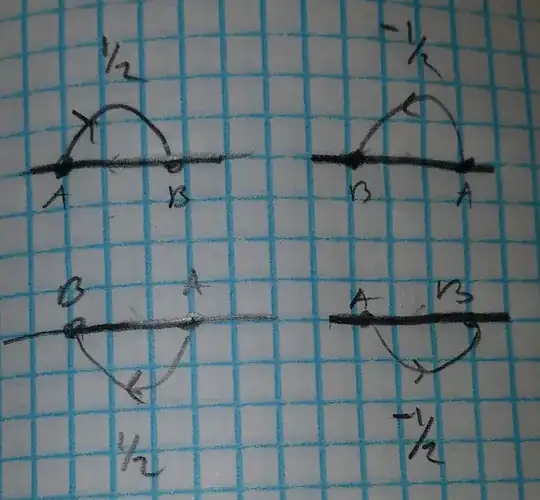
This is important because we can figure out the turning number of $\gamma$ by dividing it into arcs that go from the line to itself in one of these four cases, then adding the turning number of each arc together. However, it gives us a combinatorial description of the turning number.
We can observe that we can continuously and smoothly shift $\gamma$ so that it only turns in one direction, while still not intersecting itself - this amounts to removing instances where two oppositely oriented half turns follow each other, which is easy enough to draw out the continuous deformation that gets rid of the issue. Observe that we can do this while never introducing new intersection points.
Finally, suppose that $\gamma$ is a curve with winding number $1$ which goes from a point $A$ to a point $B$ on $\ell$. We can use the above machinery to see that there is some point $C$ on $\ell$ such that $B$ lies on the segment $AC$ where $\gamma$ (after some deformation) arcs "above" $\ell$ to get from $A$ to $C$, then "below" $\ell$ to get from $C$ to $B$ - making the sort of inwards spiral you describe - where "above" and "below" mainly refer to the sides of $\ell$ to make the turning numbers of the arcs work out right. Now we may apply this.
First, let us draw a line $\ell$ connecting $\sigma(0)$ to $\sigma(1)$. For convenience, let's assume this line is the $x$-axis and that $\sigma(1)$ is to the right of $0=\sigma(0)$ - noting that we can always rotate to get into this situation. The previous argument tells us that $\sigma$ will intersect $\ell$ at one other point $C$ to the right of $\sigma(1)$. There will be some arc above the line (or, at least above $\sigma(1)$) connecting $\sigma(0)$ to $C$. However, by periodicity, there is also an arc above the line connecting $\sigma(1)$ to $\sigma(1)+C$ - and, since $0 < \sigma(1) < C < \sigma(1)+C$, there is therefore bound to be an intersection of the image of $[0,1]$ under $\sigma$ with the image of $[1,2]$.