Set of primes $p$ which $x^4-x^3-2x^2-2x-1$ completely factors in finite field of order $p$

Question

It is known that the set of primes $p$ which the quadratic polynomial $x^2+ax+b$ factors into linear factors $\pmod p$ (or over finite field of order $p$, $GF(p)$) is a set of modular congruences. For example, the set of primes $p$ which $x^2+2x-1$ completely factors over $GF(p)$ are of the form $8y+1$ or $8y+7$.

It is also known for any cubic polynomial $x^3+ax^2+bx+c$, the set of primes $p$ for which $x^3+ax^2+bx+c$ factors into linear factors $\pmod p$ either satisfy a set of modular congruences, or can be representable by a primitive integral binary quadratic forms of discriminant equal to the discriminant of the polynomial. For example, the set of primes $p$ for which $x^3-x-1$ completely factors over $GF(p)$ are of the form $p=y^2+23z^2$.

Let $P = x^4-x^3-2x^2-2x-1$. Then what is the set of primes $p$ such that $P$ completely factors into linear factors $\pmod p$, or over $GF(p)$? It is known that this set $S$ is a modular set (linear form), quadratic form, or cubic form. Thanks for help.

The first thing to determine is what the Galois group of the polynomial is (over $\Bbb Q$). — Angina Seng, Aug 19 '18 at 07:46
I didn't go thru the algorithm but it sure looks like the Galois group is the dihedral group $D_4$. Therefore you should expect complete factorization for one eighth of the primes (asymptotically). — Jyrki Lahtonen, Aug 20 '18 at 18:52
@JyrkiLahtonen yes. I put an image from the field website, anyway the search page is at https://hobbes.la.asu.edu/NFDB/ where one may ask for degree 4 and absolute discriminant 475. The output includes the Galois group — Will Jagy, Aug 20 '18 at 19:15

Will Jagy · Accepted Answer · 2018-08-22T19:00:18.080

added. Caution: it is not a single quadratic form that represents the primes you want, it is two quadratic forms. (Monday) Indeed, we can take the two forms to be $$ x^2 + 95 y^2 \; , \; \; \; 5 x^2 + 19 y^2 \; , $$ as these represent the same odd numbers as $x^2 + xy + 24 y^2$ and $5 x^2 + 5 xy + 6 y^2;$ for either of these latter forms to be odd, we need $x(x+y)$ odd, therefore $x$ must be odd and $y$ must be even, leading to $y=2t$ and forms $(x+t)^2 + 95 t^2$ and $5(x+t)^2 + 19 t^2 \; .$

ORIGINAL:Quite surprised how this worked out. There is a 1973 article by Estes and Pall that proves that, for binary forms, the spinor kernel is the fourth powers in the form class group. At the end I have put a list up to 2000 of the relevant primes; 5 and 19 are not there, this is a simple program that just counts distinct roots mod p.

Your form discriminant is $-95,$ positive binary forms.

The forms in the principal genus that are not fourth powers are the pair of "opposites" $\langle 4,1,6 \rangle$ and $\langle 4,-1,6 \rangle.$ These represent the same primes, for which your polynomial splits as two irreducible quadratics. Added: if you prefer, you may use $\langle 9,4,11 \rangle,$ or $9x^2 + 4xy + 11 y^2,$ as it represents a subset of the same numbers, exactly the same odd numbers, and the same primes. Let's see: while it is necessary to allow $xy$ both positive and negative in searching for values of $9x^2 + 4xy + 11 y^2,$ we still get bounds on $|x|,|y|$ since $9x^2 + 4xy + 11 y^2 \geq \frac{95}{11} x^2$ and $9x^2 + 4xy + 11 y^2 \geq \frac{95}{9} y^2.$ The first few such primes are

     11,     61,    101,    139,    149,    229,    271,    311,    359,    479,
    499,    541,    571,    619,    631,    691,    701,    719,    761,    769,
    881,   1031,   1049,   1061,   1069,   1259,   1279,   1301,   1489,   1499,
   1669,   1721,   1759,   1811,   1831,   1871,   1949,   1999,   2069,   2099,
   2221,   2239,   2251,   2381,   2441,   2531,   2671,   2851,   2969,   2999,
   3049,   3079,   3089,   3121,   3209,   3331,   3361,   3389,   3659,   3691,
   3779,   3881,   3911,   4001,   4051,   4111,   4159,   4229,   4241,   4339,
   4409,   4481,   4561,   4621,   4721,   4729,   4751,   4759,   4871,   5021,
   5039,   5051,   5059,   5099,   5261,   5419,   5441,   5519,   5591,   5641,
   5659,   5669,   5701,   5711,   5801,   5839,   5849,   5869,   5939,   6011,
   6029,   6199,   6271,   6389,   6469,   6571,   6581,   6599,   6619,   6689,
   6781,   6841,   6961,   6971,   7079,   7129,   7229,   7321,   7331,   7351,
   7459,   7549,   7639,   7649,   7829,   7901,   8101,   8111,   8209,   8219,
   8231,   8269,   8291,   8329,   8369,   8521,   8669,   8689,   8741,   8941,
   8969,   9041,   9049,   9091,   9181,   9221,   9239,   9371,   9391,   9421,
   9479,   9511,   9619,   9649,   9791,   9829,   9859,  10039,  10079,  10151,
  10271,  10391,  10531,  10651,  10789,  10891,  10979,

The principal form is $\langle 1,1,24 \rangle.$ With these primes, your polynomial splits as four distinct linear factors. Added: if you prefer, you may use $\langle 1,0,95 \rangle,$ or $x^2 + 95 y^2,$ as it represents a subset of the same numbers, exactly the same odd numbers, and the same primes.

    131,    239,    389,    419,    461,    821,    859,    919,   1051,   1109,
   1531,   1601,   1879,   1901,   2011,   2399,   2411,   2609,   2699,   2791,
   2971,   3011,   3041,   3469,   3541,   3559,   3671,   3709,   4139,   4219,
   4261,   4349,   4451,   4679,   4691,   4789,   4799,   4951,   5101,   5231,
   5279,   5479,   5821,   6089,   6229,   6521,   6959,   7151,   7559,   7699,
   7759,   7949,   7951,   8081,   8179,   8461,   8599,   8681,   8719,   9011,
   9029,   9311,   9319,   9349,   9431,   9631,   9661,   9811,   9839,   9941,
  10169,  10181,  10399,  10459,  10499,  10589,  10739,  10831,  11059,  11321,
  11701,  12071,  12101,  12641,  12791,  12829,  13171,  13259,  13399,  13469,
  13649,  13681,  13729,  13799,  13841,  14029,  14411,  14419,  14779,  14869,
  15091,  15361,  15439,  15739,  15881,  15889,  15971,  16061,  16091,  16189,
  16231,  16319,  16631,  16649,  17021,  17239,  17299,  17351,  17401,  17519,
  17579,  17581,  18061,  18149,  18169,  18251,  18401,  18701,  19009,  19139,
  19301,  19609,  19709,  20261,  20411,

The other fourth power is $\langle 5,5,6 \rangle.$ This represents $5$ and $19,$ for which the polynomial has repeat roots. Other primes represented also split your polynomial into distinct linear factors. Added: if you prefer, you may use $\langle 5,0,19 \rangle,$ or $5x^2 + 19 y^2,$ as it represents a subset of the same numbers, exactly the same odd numbers, and the same primes.

      5,     19,    191,    199,    251,    349,    491,    709,    739,    809,
    929,   1151,   1201,   1289,   1429,   1451,   1559,   1619,   1621,   2039,
   2129,   2281,   2341,   2551,   2591,   2741,   2819,   2861,   3019,   3329,
   3391,   3539,   3581,   3769,   3919,   3931,   4091,   4129,   4519,   4831,
   4861,   4889,   4909,   4919,   5179,   5381,   5431,   5521,   5749,   5861,
   6091,   6211,   6659,   6661,   6761,   7001,   7039,   7069,   7369,   7411,
   7529,   7541,   7681,   8171,   8699,   8779,   8821,   8839,   8861,   9241,
   9281,   9539,   9601,   9739,   9851,   9929,  10321,  10429,  10771,  10799,
  10949,  11069,  11119,  11329,  11549,  11789,  11971,  11981,  12119,  12281,
  12451,  12671,  12689,  12841,  12889,  13001,  13249,  13309,  13339,  13499,
  13691,  13781,  13931,  14159,  14221,  14551,  14561,  14731,  14741,  14831,
  15131,  15149,  15401,  15511,  15679,  15749,  15809,  16699,  16729,  16879,
  17011,  17231,  17599,  17789,  17791,  18059,  18089,  18289,  18379,  18439,
  18541,  18859,  18959,  18979,  19289,  19391,  19501,  19861,  20071,  20149,
  20201,  20341,  20479,  20759,  20771,  20879,

Here is the form class group for discriminant $-95$

jagy@phobeusjunior:~/old drive/home/jagy/Cplusplus$ 
jagy@phobeusjunior:~/old drive/home/jagy/Cplusplus$ ./classGroup
Absolute value of discriminant? 
95
Discr  -95 = 5 * 19  class  number  8

 all  
      95:  < 1, 1, 24>    Square        95:  < 1, 1, 24>
      95:  < 2, -1, 12>    Square        95:  < 4, -1, 6>
      95:  < 2, 1, 12>    Square        95:  < 4, 1, 6>
      95:  < 3, -1, 8>    Square        95:  < 4, -1, 6>
      95:  < 3, 1, 8>    Square        95:  < 4, 1, 6>
      95:  < 4, -1, 6>    Square        95:  < 5, 5, 6>
      95:  < 4, 1, 6>    Square        95:  < 5, 5, 6>
      95:  < 5, 5, 6>    Square        95:  < 1, 1, 24>

 squares  
      95:  < 1, 1, 24>
      95:  < 4, -1, 6>
      95:  < 4, 1, 6>
      95:  < 5, 5, 6>

 fourths  
      95:  < 1, 1, 24>
      95:  < 5, 5, 6>


Discriminant        -95     h :    8     Squares :    4     Fourths :    2
jagy@phobeusjunior:~/old drive/home/jagy/Cplusplus$

=====================================

These are the first few primes (NOT $5,19$ because they have repeated roots) for which the polynomial has four distinct roots.

jagy@phobeusjunior:~$  ./count_roots   
131  count   1
191  count   2
199  count   3
239  count   4
251  count   5
349  count   6
389  count   7
419  count   8
461  count   9
491  count   10
709  count   11
739  count   12
809  count   13
821  count   14
859  count   15
919  count   16
929  count   17
1051  count   18
1109  count   19
1151  count   20
1201  count   21
1289  count   22
1429  count   23
1451  count   24
1531  count   25
1559  count   26
1601  count   27
1619  count   28
1621  count   29
1879  count   30
1901  count   31
2011  count   32

Note that the version of the polynomial used on the field website is something like $ -x^4 \cdot f\left(\frac{-1}{x}\right)$

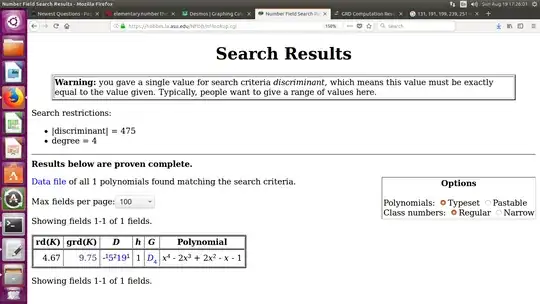
Added Monday lunchtime: perhaps a little more attractive to say the primes giving four linear factors are represented by the two forms $$ x^2 + 95 y^2 \; , \; \; \; 5 x^2 + 19 y^2 \; , $$ while the primes that give two irreducible quadratic are represented by $$ 9 x^2 \pm 4xy + 11 y^2 $$

Curious of the splitting forms, I found that the class number of the field $K = \mathbb{Q}(\sqrt{-95})$ is $8$ and its defining Hilbert class field is $H = \mathbb{Q}(r)$ where $r$ is a root of the polynomial $x^8-x^6+2x^5+3x^4-x^3-x^2-x-1$. The primes that completely split in $F$ have the form $x^2+95y^2$, compared to the two quadratic forms for primes splitting in $H' = \mathbb{Q}(r')$ were $r'$ is a root of the original polynomial in this problem. — J. Linne, Aug 23 '18 at 00:56
To conclude all of this, $H'$ is a proper subfield of $H$, referring to the information in my last comment. — J. Linne, Aug 23 '18 at 00:57
Dear Will Jagy, and dear @Jyrki Lahtonen , regarding the second paragraph of the main question: I am not sure if this is true or not. Theorem: Let $a$ be a positive integer and let $K=\mathbb{Q}(\sqrt{-a})$, then $\mathbb{Z}[{\sqrt{-a}}]$ is an order in the ring of integers $\mathcal{O}_k$, then there exist a polynomial $f_a(x)$ of degree $h(-4a)$, such that an odd prime $p \nmid 2a Disc(f_a(x))$ is representable by the quadratic form $y^2+az^2$ iff both of the equations $x^2+a \cong 0$ and $f_a(x) \cong 0$ have a solution modulo $p$. — Davood, May 19 '20 at 12:21
Dear Will Jagy, and dear @Jyrki Lahtonen , regarding the second paragraph of the main question: If we were restricted just to the case $a \geq 1$, then it is not true. If the second paragraph is true, then there exists infinitely many $a \in \mathbb{Z}$ such that $h(-4a)=3$, but for positive $a$'s it is not true. But we were not restricted to the positive case, and this argument does not work for the negative case, But if the claim in the second paragraph is true, could you please introduce me a reference on the subject? — Davood, May 19 '20 at 12:23
@DavoodKHAJEHPOUR the main reference is D. A. Cox, Primes of the form $x^2 + n y^2.$ Then article http://zakuski.utsa.edu/~jagy/Hudson_Williams_1991.pdf My feeling is that the second paragraph is too optimistic. I will look for an example. — Will Jagy, May 19 '20 at 16:40
@DavoodKHAJEHPOUR for cubic $x^3- x^2 +2x +1,$ ignoring primes $2,3,29,$ the primes giving complete factoring are $p = x^2 + xy + 22y^2$ and $p= 3x^2 + 3xy + 8y^2$ — Will Jagy, May 19 '20 at 17:03
Dear @WillJagy , I find the paper that you've been introduced very interesting. But I should apologize for not asking my question very clear. By the "second paragraph of the main question" I meant this paragraph: "It is also known for any cubic polynomial* $x^3+ax^2+bx+c$, the set of primes $p$ for which $x^3+ax^2+bx+c$ factors into linear factors $\pmod p$ either satisfy a set of modular congruences, or can be written in some quadratic form $p=y^2+az^2$ for some integer $a$.*" Sorry again for not being clear dear will Jagy — Davood, May 19 '20 at 19:21
@DavoodKHAJEHPOUR suggest you spend some time working out, for example, why $x^3 - x^2 + 2x +1$ does not satisfy you, then post a new question. The Theorem you quote in your first comment is very close to Theorem 9.12 on page 180 of Cox. (Well, page 180 in the first edition) — Will Jagy, May 19 '20 at 20:11
The forms can be replaced by $x^2 + 87 y^2 $ and $3x^2 + 29 y^2$ — Will Jagy, May 19 '20 at 20:17
Dear @WillJagy I read the interesting book Primes of the form $x^+ny^2$ by David Cox, and I posted this theorem form that book, but I forgot to mention it in the 3 previous mentions. My question is answered by the theorem 1 and 2 in this paper (which is referenced back to this paper). Thank you so much for your patience, dear Will Jagy. — Davood, May 19 '20 at 21:55
Dear @WillJagy, In the second paragraph of the main question it is written that: "It is also known for any cubic polynomial $x^3+ax^2+bx+c$, the set of primes $p$ for which $x^3+ax^2+bx+c$ factors into linear factors $\pmod p$ either satisfy a set of modular congruences, or can be written in some quadratic form $p=y^2+az^2$ for some integer $a$." But by looking at this paper, we can just conclude that $p$ is representable by some quadratic form, not necessarily the principal form. — Davood, May 19 '20 at 22:08

Set of primes $p$ which $x^4-x^3-2x^2-2x-1$ completely factors in finite field of order $p$

1 Answers1

Linked