Let $n,m\in\mathbb{Z}$ with $0 \le 2m < n$. Let $X_1, \cdots, X_n$ be i.i.d. standard Gaussians and let $X_{(1)} \le X_{(2)} \le \cdots \le X_{(n)}$ denote their order statistics (i.e., $\{X_1, X_2, \cdots, X_n\} = \{X_{(1)}, X_{(2)}, \cdots, X_{(n)}\}$). Define $$Y=\frac{X_{(m+1)} + X_{(m+2)} + \cdots + X_{(n-m)}}{n-2m}.$$ Clearly, by symmetry, $\mathbb{E}[Y]=0$. What can we say about $\mathsf{Var}[Y]=\mathbb{E}[Y^2]$?
A closed-form expression for $\mathbb{E}[Y^2]$ for all $n$ and $m$ is too much to ask for. Ideally, I want explicit and reasonably tight upper (and lower) bounds. I have the following conjecture I would like to prove.
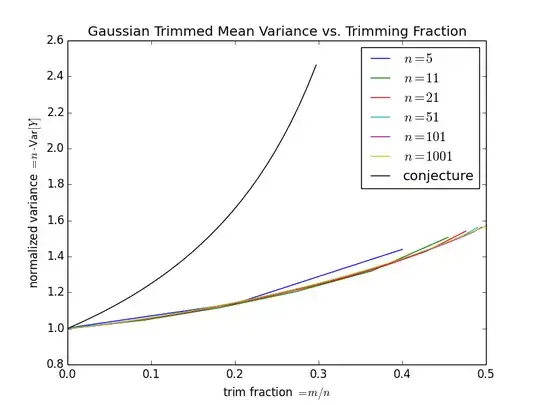
Conjecture. $$\mathbb{E}[Y^2] \le \frac{1}{n-2m}$$
This is obviously true for $m=0$ and also holds for $m=(n-1)/2$. The intuition for this is that $Y$ is essentially the average of $n-2m$ standard Gaussians, except the distribution has had its tail amputated, which should only reduce variance.
More generally, I am looking for a bound of the form $$\exists a,b,c\in(0,\infty) ~~~~\forall n \ge b \cdot m \ge a ~~~~~~~~ \mathbb{E}[Y^2] \le \frac{1}{n}\left( 1 + c \cdot \frac{m}{n}\right)~~~~~~~~~~.$$ I want the constants $a,b,c$ to be explicit and as small as possible.
I'm interested in the asymptotics as $n,m \to \infty$ and $\frac{m}{n} \to 0$. For example, $m=\log n$ is a parameter regime that interests me.
The asymptotic answer as $n\to\infty$ while $m/n \to \alpha>0$ has been studied.
Below are some numerical results (based on the average of $10^6$ draws). The trimmed mean smoothly interpolates between the mean (variance $1/n$) and the median (asymptotic variance $\pi/2n \approx 1.57/n$). Clearly one could hope for better than the conjecture.
The interpretation of this question is as follows. I have $n$ samples from a normal distribution and I discard the largest $m$ samples and the smallest $m$ samples as "outliers". I estimate the mean of the distribution using the remaining samples. This is apparently known as the truncated mean or trimmed mean.
The question is what is the mean squared error of this estimator? That is, how much does discarding supposed outliers hurt? (Without loss of generality, for the analysis, I can assume zero mean and unit variance, even though these values would be unknown in practice.)
Ideally I want a result that holds for all "nice" distributions. Nice could mean something like symmetric, continuous, light-tailed, and unimodal. However, any definition of nice should include the Gaussian.