in calculating the area of a circle in a square we use random points to calculate the fraction of circle! but why we dont assume a simple grid and put our points in the center of it. this seems more uniform and the result should be better.
-
Pseudorandom numbers sort of do what you are describing. – Calculon Jul 30 '18 at 08:58
-
1In high dimensions you may not have enough points to form a meaningful grid, but Monte Carlo methods may still provide a decent approximation – Henry Jul 30 '18 at 09:05
-
1See "Why use Monte Carlo method instead of a simple grid?" on the statistics StackExchange. – Jul 30 '18 at 09:07
1 Answers
When you are doing one-dimensional integration, you are right. It is often more efficient to use a grid of evenly spaced points in the interval of integration. (There are a few periodic functions and other special cases in which the Monte Carlo method with randomly chosen points is better in one dimension.)
However, in multiple dimensions the Monte Carlo approach is very often better. Suppose you want to integrate an uncorrelated standard bivariate normal distribution (means 0, SDs 1, correlation 0) over the triangle $T$ with vertices at $(0,0), (0,1), (1,0).$ If you try to use a 2-dimensional grid of points that serve as the centers of bases of 'posts' that extend from the plane upward to the surface of the density, you will not only have 'raggedy' edges where the posts meet the density surface, you will also have raggedy edges along the hypotenuse of the triangle. You will need very many grid points to get a good approximation.
However, if you generate points uniformly at random within the triangle, you will do about as well or better with the same number of points in a grid. The random points are 'unpredictable' but they fit nicely into the triangle.
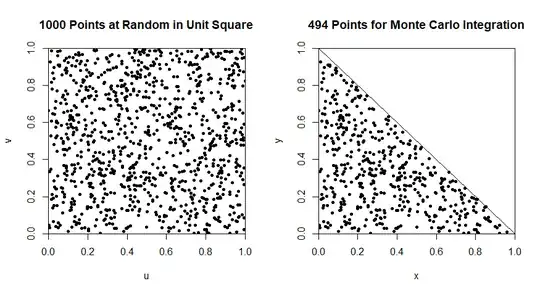
Example: In the following simulation in R statistical software, $m = 1000$ points are generated in the unit square, of which about 500 within the triangle $T$ are used. For $(X,Y)$ distributed according to this bivariate normal distribution, $P[(X,Y)\in T]$ is approximated as 0.06776, whereas one can show by a geometric argument that this particular probability is exactly 0.06773.
set.seed(818); m = 10^3
u = runif(m); v = runif(m); keep = (u + v < 1)
x = u[keep]; y = v[keep]
.5*mean(dnorm(x)*dnorm(y))
[1] 0.06776174
Integrating over regions of dimension greater than two, the raggedy hyper-edges proliferate if you use a multi-dimensional grid. Then the Monte Carlo method is almost always better than a grid.
That said, it must be admitted that one can always contrive multi-dimensional integrations for which a regular grid happens to work best. Just as you can contrive one-dimensional functions for which the Monte Carlo method works best. Factors include the 'smoothness' of the function and the 'smoothness' of the boundaries of the region of integration.
- 52,418