Prove that: Probability of connectivity of a random graph is increasing with the size of the graph

Question

In a random graph $G(n, p)$, the exact probability of the graph being connected can be written as: $$ f(n) = 1-\sum\limits_{i=1}^{n-1}f(i){n-1 \choose i-1}(1-p)^{i(n-i)} $$

This probability is claimed to converge to 1, when $n \rightarrow +\infty$. Empirically simulating this function, indeed it converges to 1, for different values of $p$.

Additionally, I conjecture that this function is an strictly increasing with $n$ (for $n > 2$ and $p > 0.5$). Any thoughts on how we can prove/disprove this conjecture?

---

Here is an effort:

If I prove that $f(n) - f(n-1) > 0$ for any $n > 2$, I'm done (proving that it's strictly increasing). $$ f(n) - f(n-1) = \left(1-\sum\limits_{i=1}^{n-1}f(i){n-1 \choose i-1}(1-p)^{i(n-i)} \right) - \left(1-\sum\limits_{i=1}^{n-2}f(i){n-2 \choose i-1}(1-p)^{i(n-1-i)} \right) \\ = \sum\limits_{i=1}^{n-2}f(i){n-2 \choose i-1}(1-p)^{i(n-1-i)} - \sum\limits_{i=1}^{n-1}f(i){n-1 \choose i-1}(1-p)^{i(n-i)} \\ = \sum\limits_{i=1}^{n-2}f(i){n-2 \choose i-1}(1-p)^{i(n-1-i)} - \sum\limits_{i=1}^{n-2}f(i){n-1 \choose i-1}(1-p)^{i(n-i)} - (n-1) \cdot f(n-1)(1-p)^{n-1} \\ = \sum\limits_{i=1}^{n-2}f(i){n-2 \choose i-1}(1-p)^{i(n-1-i)} - \sum\limits_{i=1}^{n-2}f(i){n-2 \choose i-1}(1-p)^{i(n-1-i)} \times \frac{n-1}{n-i} (1-p)^{i} - (n-1) \cdot f(n-1)(1-p)^{n-1} \\ = \left\lbrace \sum\limits_{i=1}^{n-2}f(i){n-2 \choose i-1}(1-p)^{i(n-1-i)} \times \left[ 1 - \frac{n-1}{n-i} (1-p)^{i}\right] \right\rbrace - (n-1) \cdot f(n-1)(1-p)^{n-1} \\ $$

Since $p > 0.5$, $1-p < 0.5$ and $\frac{n-1}{n-i} (1-p)^{i} < 1$ (for any $i$). Hence the first term is positive. However, this is not enough for proving the strict increasing behavior of $f(n)$; we have to show that this is first term is strictly biggeer than the 2nd (negative) term.

Let's try the first few terms. One can see that the first few terms of this function is ($q = 1-p$): $$ f(2) = 1-q \\ f(3) = 1 - 3q^2 + 2q^3 \\ f(4) = 1 - 4q^3 - 3q^4 + 12q^5 - 6q^6 \\ f(5) = 1 - 5q^4 - 10q^6 + 20q^7 + 30q^8 - 60q^9 + 24q^{10} \\ $$

Here I plot the differences $f(i) - f(i-1)$: $$ f(3) - f(2) = -3q^2 + 2q3 + q $$

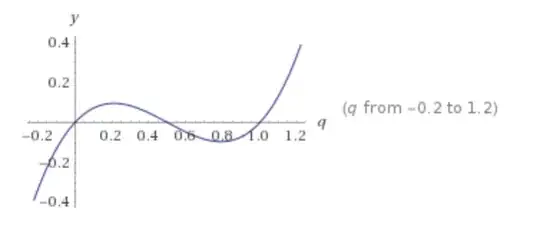
$$ f(4) - f(3) = - 4q^3 - 3q^4 + 12q^5 - 6q^6 - (- 3q^2 + 2q^3) $$

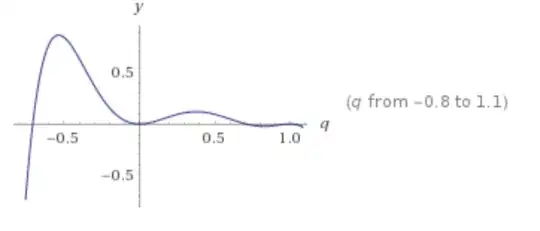
$$ f(5) - f(4) = - 5q^4 - 10q^6 + 20q^7 + 30q^8 - 60q^9 + 24q^{10} - (- 4q^3 - 3q^4 + 12q^5 - 6q^6) $$

Visuallly all the difference functions are positive for $q < 0.5 (i.e. $p > 0.5$)$ (i.e. conjecture is supported).

Answer 1

There are two facts about the probability of connectedness that have nice clean proofs, which we'll use as lemmas.

1. The probability is increasing in $p$. This is because if $p < p'$, we can view a random graph with edge probability $p'$ as the union of two random graphs; one with edge probability $p$, and one with edge probability $\frac{p'-p}{1-p}$. The union is connected if either graph is connected.
2. The probability is at least $\frac12$ when $p \ge \frac12$. This is because if $p = \frac12$, both the random graph $G$ and its complement $\overline{G}$ are random graphs with edge probability $\frac12$, and we know that at least one of them is always connected. This would be impossible if the probability were less than $\frac12$. For $p>\frac12$, use the first fact.

Now let $G$ be a random graph with $n$ vertices $v_1, \dots, v_n$ and edge probability $p$, and let $G'$ be obtained from $G$ by adding another vertex $v_{n+1}$ adjacent to each vertex of $G$ independently with probability $p$. To prove $f(n+1) > f(n)$, we'll prove that $\Pr[G' \text{ is connected}] > \Pr[G \text{ is connected}]$.

This only requires comparing two events. First, the event that $G$ is connected but $G'$ is not, which we'll call $\mathsf{DOWN}$. Second, the event that $G$ is not connected, but $G'$ is, which we'll call $\mathsf{UP}$. We want to show that $\Pr[\mathsf{UP}] > \Pr[\mathsf{DOWN}]$.

An upper bound on $\Pr[\mathsf{DOWN}]$ is $(1-p)^n$. This is because if $G$ is connected but $G'$ is not, no vertex of $G$ can be adjacent to $v_{n+1}$.

For a lower bound on $\Pr[\mathsf{UP}]$ consider the $n$ disjoint events where, for $i=1,\dots,n$, vertex $v_i$ in $G$ is isolated, all other vertices of $G$ are connected, and $v_{n+1}$ is adjacent to both $v_i$ and $v_{i+1}$ (wrapping around if $i=n$). These each have probability $f(n-1) \cdot (1-p)^{n-1} \cdot p^2$, which is at least $\frac18 \cdot (1-p)^{n-1}$ (using the second fact as a lower bound on $f(n-1)$), so $\Pr[\mathsf{UP}] \ge \frac n8 \cdot (1-p)^{n-1}$.

The inequality $$ \frac n8 \cdot (1-p)^{n-1} > (1-p)^n $$ holds whenever $n \ge 4$, since $1-p < \frac12$, and implies that $\Pr[\mathsf{UP}] > \Pr[\mathsf{DOWN}]$.

This shows that for $n\ge 4$, $f(n+1) > f(n)$. We still need to check that $f(4) > f(3) > f(2)$; that is, $p < 3p^2-2p^3 < 16p^3 - 33p^4 + 24p^5 - 6p^6$ when $\frac12 < p < 1$. This can be done manually:

• $f(4)-f(3)$ factors as $-3p^2(1-p)^2(1-4p+2p^2)$, so it's positive when $1 - \frac{\sqrt2}{2} < p < 1$.
• $f(3)-f(2)$ factors as $-p(1-p)(1-2p)$, so it's positive when $\frac12 < p < 1$.